Differential privacy, secure multiparty computation, and homomorphic encryption

Main article: Privacy, identity, and fraud in the ratings system

Differential privacy

Differential privacy (DP) is a technique used to anonymize datasets with personal or sensitive information. In DP we introduce some statistical noise into the answer each person gives in a way that gives that person plausible deniability while still providing a reliable aggregate statistic (eg an average).

The simple example given to beginners is to imagine a college giving a survey to its students asking them if they’ve ever cheated on a test. The college assures the students that they don’t have to provide their names so their answers will be completely anonymous. But this is not secure because the college also asks other identifying questions, like year, major, gender, etc., which could be used to identify individuals. So the students, fearing they may be summoned to the honor court if they report having cheated, are not happy with the survey.

The better way for the college to ensure privacy is to suggest to the students that they answer the question as follows: flip a coin and if it’s heads answer the question honestly. If tails, flip the coin again and answer honestly if it’s heads and dishonestly if its tails. So the cheater who flips two tails in a row answers that they never cheated and the non-cheater doing the same answers that they have cheated. So we end up with 25% of the respondents answering the question dishonestly. Now if the college tries to identify and prosecute a cheater, the student can claim plausibly that they were simply following the coin toss instructions and are part of the 25%.

But how is the college to get an accurate aggregate statistic when 25% of the students effectively lied? From the resulting dataset they can back-calculate the correct number using the following equation:

${\textstyle F_{c}=0.75c+0.25(1-c)}$

where

${\textstyle F_{c}}$ is the fraction of reported cheaters in the dataset

${\textstyle c}$ is the fraction of true cheaters

To put this in words, the fraction of cheaters in the dataset ( ${\textstyle F_{c}}$ ) is the fraction of true cheaters, those cheaters who answer honestly ( ${\textstyle 0.75c}$ ) plus the fraction of non-cheaters who answer dishonestly ( ${\textstyle 0.25(1-c)}$ ). Now we can solve for ${\textstyle c}$ , providing us with an estimate of the fraction of cheaters from ${\textstyle F_{c}}$ , the fraction who answered that they cheated:

${\textstyle c=2F_{c}-0.5}$

It’s important to keep in mind that these are probabilities which become more accurate as we increase the size of the dataset.

This example is explained at length here.

Now let’s do something similar with our example above where several people are asked to rate someone on, say, financial accounting on a scale of 0-10. We will randomly ask 25% of the raters to provide a random answer (0-10) instead of their real answer. Now, any rater who is identified can plausibly claim that their answer was random.

This situation is not as clean as the one above where there were only two answers. In the cheater/no-cheater case anyone who changes their answer only has one other choice. This narrows down the possibilities considerably and makes for a very simple, and accurate, equation for back-calculation.

In the ratings case the “dishonest” rater can randomly pick any integer between 0-10. For a statistically valid sample size, the average of the dishonest ratings will be 5. Meanwhile the average of the honest ratings can be anything in the 0-10 range. If the average of the honest ratings is higher than 5 we can surmise that the dishonest ratings are too low. This is based on the assumption that the dishonest ratings should have been about the same average as the honest ones. Similarly, if the average of the honest ratings is lower than 5 we surmise that the dishonest ratings are too high.

With this in mind, we can derive an equation to correct a dataset with dishonest answers. Suppose the total population is ${\textstyle N=100}$ and 25% of them are asked to provide a random answer instead of the truth. Thus 25 people rated randomly and we can expect the average of their answers to be around 5. Let’s suppose the average of the honest raters is 8. So we assume that our dishonest average is low and skews the overall average toward the low side. Let’s call this overall raw average the “privacy average”, ${\textstyle PA}$ .

${\textstyle PA={75(8)+25(5) \over 100}=7.25}$

Since we want an average of 8 (assuming it’s the same as the honest raters), we correct it as follows:

${\textstyle CA={75(8)+25(5)+25(8-5) \over 100}={PA+{25(8-5) \over 100}}=8}$

where

${\textstyle CA}$ is the corrected average

Note that ${\textstyle CA=8}$ , so

${\textstyle PA+{25(CA-5) \over 100}=CA}$

We can now solve for ${\textstyle CA}$ in terms of ${\textstyle PA}$ :

${\textstyle PA+{25CA \over 100}-{25(5) \over 100}=CA}$

${\textstyle CA(1-{25 \over 100})=PA-{25(5) \over 100}}$

${\textstyle CA={PA-{25(5) \over 100} \over {1-{25 \over 100}}}}$

Note that 25/100 is simply the fraction of dishonest raters which we set at 25%. We can call this ${\textstyle F_{d}}$ to generalize it. And 5 is the average of the dishonest ratings which we can call ${\textstyle A_{d}}$ to generalize. Our formula is now

${\textstyle CA={{PA-{F_{d}}{A_{d}}} \over {1-F_{d}}}}$

where

${\textstyle F_{d}}$ is the fraction of dishonest raters (eg 0.25 in example above).

${\textstyle A_{d}}$ is the average of dishonest raters (eg 5 in example above).

Thus, knowing any privacy average, fraction of dishonest raters (which we set), and average of dishonest ratings (eg 5 or the midpoint of the range of ratings used) we can find a corrected average.

Keep in mind that these corrections are only statistically accurate, not rigorously so. In a small dataset they may include considerable error. This is why we accept, as the price of privacy, that the aggregate will have some error in it. However, since aggregate numbers often don’t have to be that precise, this is an acceptable tradeoff.

One important property of DP is that it ensures that any new rating that appears in the dataset reveals no information about the rater. Suppose, with no DP, we have the average of a dataset composed of 100 values. A new person then decides to send in their rating to make the number of values 101. A new average is calculated (again, no DP). However, by knowing the new average and the old average we can easily calculate what that new person gave as their rating. But with DP this calculation does not reveal any reliable information about the rater.

DP is an active field of research and the examples shown here only scratch the surface. A few references to work in this area:

Other privacy techniques (not necessarily DP):

Error in Differential Privacy

Let’s return to the problem where we’ve asked some people to rate Pete, say, on his financial accounting skills. The raters don’t want to reveal their individual scores. Pete, however, will see the aggregate and that’s ok with the raters because we will use a differential privacy (DP) scheme.

Above we produced a general equation for correcting a differential privacy method:

${\textstyle CA={{PA-{F_{d}}{A_{d}}} \over {1-F_{d}}}}$

where

${\textstyle F_{d}}$ is the fraction of dishonest raters.

${\textstyle A_{d}}$ is the average of dishonest raters.

${\textstyle PA}$ is the privacy average, or raw average including the dishonest answers.

${\textstyle CA}$ is the corrected average.

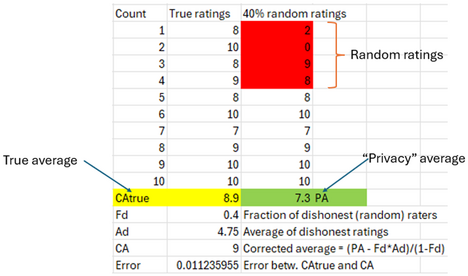
Let’s do a concrete example of this scheme to understand it better and then analyze the error associated with it. Unlike above where we had ${\textstyle N=100}$ , let’s try a case with fewer people, ${\textstyle N=10}$ , since that is probably more representative of Pete’s raters. Let’s say the fraction of raters asked to provide a random number ( ${\textstyle F_{d}}$ ), ie the fraction of “dishonest” raters, is 40%. So the first 4 raters are asked to rate at random, anywhere between 0-10 including the end points and everyone else rates honestly. Let’s assume further that the honest ratings have an average of 8, so the presence of the random raters will probably skew the average low (since on average their rating will be 5).

The following spreadsheet shows one possible result:

The error between the true average ( ${\textstyle CA_{true}}$ ) and ${\textstyle CA}$ is 1.1%. This seems quite good given the low number of raters and the fairly hefty number who answered randomly.

But this is only one result and maybe we just got lucky. Let’s try to calculate the error by running this case 1000 times (say) and calculating the average error. The attached Python snippet does this and, sure enough, reveals an error that is higher, at 3.7%. Still, this also seems fairly encouraging given the low number of samples and high fraction of random raters.

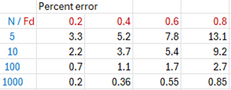
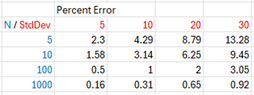
We can do this for several combinations of ${\textstyle F_{d}}$ (fraction of sample that answers dishonestly or randomly) and ${\textstyle N}$ (population size):

Here we find that for ${\textstyle N=5}$ and ${\textstyle F_{d}=0.8}$ we obtain an error of 13.1%. We might ask how this is possible since a solid majority of the raters were dishonest. To answer this let’s assume that all the raters had been dishonest ( ${\textstyle F_{d}=1}$ ). This case isn’t shown here because there is no way to calculate ${\textstyle CA}$ since the denominator in the equation

${\textstyle CA={{PA-{F_{d}}{A_{d}}} \over {1-F_{d}}}}$

is zero.

Instead we can multiply both sides of the equation by ${\textstyle 1-F_{d}}$ and reach the obvious conclusion that ${\textstyle PA=A_{d}}$ . So the only two useful numbers we have are the average of the dishonest ratings, which should be around 5 and the average of what they would have been if they were allowed to rate honestly, which should come to around 8. So the highest possible error in this scheme is

${\textstyle (8-5)/8=0.375}$

Or 37.5%. No error, therefore, can be higher than this. So, in a sense, we are biasing our errors toward the low side. We could recreate the table above again by calculating the fraction of this maximum error that each error represents, and express this as a percentage:

The errors don’t look so great anymore. We can go further and realize that in any scenario involving a 0-10 rating, that the maximum possible error is 50%. This is because the average rating will always be around 5 and the maximum either a 10 or a 0. In either case the error is 50%.

Curiously, the error depends strongly on the average rating itself. If someone rates at either end of the 0-10 spectrum, the error is high. But if someone has an average honest rating of 5, then the error is 0 even if all raters rate randomly. A rating of 5 means that it makes no difference if the raters rated honestly or randomly.

Despite all this, it is clear that differential privacy works even on smaller datasets with substantial fractions of random ratings. It will be important to clarify to users exactly what the errors are, and what they mean, when using this technique.

Differential Privacy (DP) and Normal Distributions

One of the downsides of the DP scheme we discussed above was that some of the raters, most in fact, had to provide their honest ratings. Although everyone could claim deniability, if it became known somehow who the honest raters were, this advantage would disappear. Here we discuss a scheme where all the raters provide random ratings so they all have true deniability.

The scheme works by telling the raters to provide a random number within a normal distribution centered about their true rating. We suspect that doing this will lead to some ratings higher and some lower than the true rating but, on average, will match the true rating fairly closely. Therefore there wouldn’t be any need for correcting the average result. Indeed, there would be no basis for correcting the result because the statistical noise is always centered about the average.

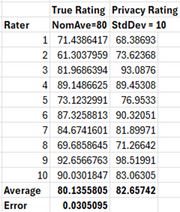
As an example, let’s take a single case with a population of 10 raters and a 0-100 ratings scale. Let’s suppose the nominal average rating is 80. Each rater has a True Rating but then runs a random number generator to alter that with a normal distribution (say) with a mean set to the true rating and a standard deviation of 10 (say). We will call the altered rating the Privacy Rating. The following table gives one possible result:

This is reasonable. The average rating and the privacy rating are somewhere close to 80, even for this statistically small sample. And the raters are given a healthy margin by which to alter their results. For this case the error is about 3% which seems acceptable for statistical purposes.

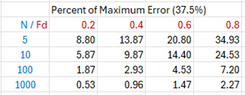
But this is only a single case and a more rigorous error analysis is necessary to prove that the method works and to understand the tradeoffs associated with it. The attached Python snippet performs this analysis, in a similar way as above. It runs each set of ratings, as seen in the table above, 1000 times to ensure that we are getting a proper average of the errors. The following table provides these errors for various population sizes and standard deviations:

Again, along with the results above, we can be pleasantly surprised by this. Unless the population size becomes very small with a large standard deviation, the errors are reasonable. For large populations they become negligible.

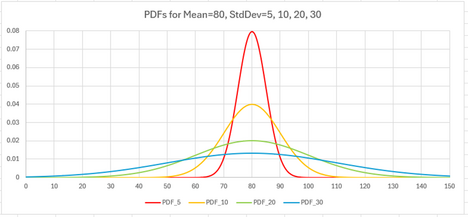
As a matter of visualization and understanding, we might draw a graph of what the standard deviation looks like for these cases. One standard deviation means that about 68% of the results will lie within it, centered about the mean. Two standard deviations means that about 96% of results lie within it and 3 means greater than 99%. So here, when we speak of a standard deviation of 10, we mean that 68% of the results lie between +-10 of the mean, so between 70 and 90.

In this case, as a practical matter, StdDev = 5 is somewhat constrained in terms of its plausible deniability but above that we have quite a wide practical range.

We note that the rating on the x-axis goes up to 150, far beyond the 100 we stipulated as the maximum for this scale. This is only for illustration. In practice, anyone whose random rating is calculated to be above 100 would just pick 100. Similarly, if the mean rating had been below 50, the larger standard deviations would produce ranges extending well below 0. In this case the rater would just pick 0.

The Python snippet mentioned above has the ability to either cut off the scale at 0 or 100 or to let the scale float above/below these values as shown on the graph. The table above calculates the errors with the floating scale since this gives us mathematically precise error values. Cutting the scale off artificially obfuscates the error needlessly. Our purpose here is to demonstrate the efficacy of the method and this demands an accurate representation of the error.

Here is an attachment to the Excel spreadsheet the tables and graphs came from: Brainstorming_21.xlsx

Secure Multiparty Computation (SMC)

SMC is a method by which a group can perform some mathematical operation on shared data without anyone knowing the data of anyone else. The classical example of this is the Millionaires’ Problem in which Alice who has $8 million and Bob who has $5 million wish to know who is richer without revealing how much each one has. This problem was solved by Yao, among others, and this reference provides an explanation for how this is done.

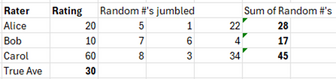
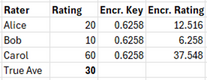
Let’s apply a version of SMC more suited to our case using a very simple example. Three people, Alice, Bob, and Carol wish to know their average rating without revealing to the others what their own rating is. To make the numbers easier, let’s assume the ratings scale is 0-100. Each person’s real rating is (20, 10, 60) for an average of 30. They start by randomly selecting 3 numbers that add up to their rating:

Then they jumble the numbers such that each of the three raters gives 2 of their random numbers to the others:

Notice that this exchange provides no helpful information to each rater in figuring out another rater’s rating.

Now each rater has 3 random numbers and proceeds to add them up:

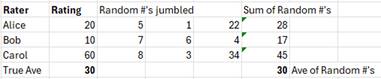
If we then take the sum of these sums and calculate the average, we obtain the true average:

Now the group knows the average but no one in the group knows any other member’s rating but their own.

This variant of SMC does not work, of course if there are only two raters. If two people want to compute an average of their two ratings, there is no way they won’t be able to determine the other person’s rating. This scenario is the same as simply asking the other person for their rating.

The example shown here was taken from inpher which provides commercial tools for both SMC and HE and also provides an open source library for HE and makes it available on github.

Other SMC references:

https://www.sciencedirect.com/science/article/abs/pii/S0167404823000524

https://link.springer.com/article/10.1186/s13059-022-02841-5

https://www.researchgate.net/profile/Joseph-Oluwaseyi-2/publication/379409115_Secure_Multi-Party_Computation_MPC_Privacy-preserving_protocols_enabling_collaborative_computation_without_revealing_individual_inputs_ensuring_AI_privacy/links/66076488390c214cfd24b406/Secure-Multi-Party-Computation-MPC-Privacy-preserving-protocols-enabling-collaborative-computation-without-revealing-individual-inputs-ensuring-AI-privacy.pdf

Homomorphic Encryption (HE)

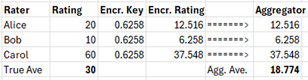
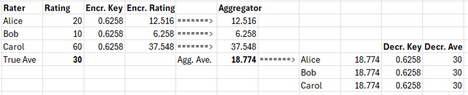
Let’s suppose this same group of 3 wants to send their ratings to an aggregator in an encrypted form, have the aggregator perform the average over the encrypted values, obtain an encrypted average, and send back the result to the group. The aggregator does nothing but perform as a calculator in this case and knows nothing about the data. Let’s say the true ratings are again (20, 10, 60) which averages out to 30. They each encrypt their rating with the following simple key: multiply the rating by 0.6258.

For each rating, we obtain using this simplistic formula the values (12.516, 6.258, 37.548) and send these to the aggregator who computes the average, 18.774:

This value is sent back to each member of the group who decrypt it by dividing it by the key, 0.6258, to obtain the average, 30, which matches the known true average.

The aggregator, in principle, knows nothing about the real numbers since he doesn’t know the encryption key. All he can do is perform the average on the numbers he is given, which are encrypted. The individuals in the group, meanwhile, only know the average, not the ratings given by the other members.

Homomorphism is the property of structure preservation in a mapping. If we map our original ratings to encrypted ones, the encrypted ones preserve the same structure, and basic relationship between members, that the original ones had. This means, among other things, that if a number ${\textstyle a>b}$ in the original set that it continues to be in the homomorphically encrypted set, ie ${\textstyle a_{e}>b_{e}}$ . Obviously a simplistic mapping like multiplying by a constant will be homomorphic. But much more complex mappings are homomorphic as well.

We might be worried here about the aggregator being dishonest and reporting back a junk number. A simple way to handle this is to use more than one aggregator and see if they agree.

We may also be worried about a hacker who intercepts the encrypted numbers from the group to the aggregator and replaces them with fake numbers. Again, we could use more than one aggregator to lessen the likelihood that the hacker would intercept all the numbers. But let’s suppose we aren’t satisfied with this and want more certainty.

The group could, perhaps, embed a verification sequence within the encrypted numbers. For example they could agree to add 4 random numbers that add up to 10 to each of the numbers they sent to the aggregator, eg (12.5164303, 6.2582314, 37.5486121). Now they could ask the aggregator to provide the last 4 digits of each number back to them. If the aggregator received a hacked number it is highly likely that it would not include a last-four sequence that adds up to 10. There is some possibility, of course, that the aggregator himself is dishonest and, knowing that the last 4 digits is important, proceeds to figure out the verification sequence. But even so, if the aggregator is to do serious harm, he would have to change the numbers substantially, a problem which, as noted above, can be solved by having more than one aggregator.

Homomorphic encryption is obviously more complex than this naïve example suggests. Clearly every mechanism shown here is so simple that a decent cryptologist could figure it out. Indeed, real HE is so complex that one of its limiting problems is computational cost. We provide the example only to get a feel for what HE is and examine some possibilities in its application. More references on HE can be found here:

https://link.springer.com/article/10.1007/s11227-023-05233-z

https://link.springer.com/chapter/10.1007/978-3-030-77287-1_2

https://link.springer.com/chapter/10.1007/978-3-319-12229-8_2

https://dl.acm.org/doi/abs/10.1145/2046660.2046682

https://digitalprivacy.ieee.org/publications/topics/what-is-homomorphic-encryption

https://www.keyfactor.com/blog/what-is-homomorphic-encryption/

https://www.internetsociety.org/resources/doc/2023/homomorphic-encryption/

The Problem of Collusion

Regardless of the method, it is difficult to prevent collusion from exposing a single person’s rating. Suppose that, in the above scenarios, Alice and Carol wish to learn Bob’s rating. They can collude to tell each other their rating, or collude to provide a fake rating and tell each other that. After the average is computed, Alice and Carol can easily back-calculate Bob’s rating from the average and their own two ratings. Or, using a more direct approach, perhaps they collude with the aggregator who simply gives them all his encrypted ratings. There doesn’t appear to be any way to prevent this. Certainly neither SMC or HE, on their own, will solve this problem.

Differential privacy, however, offers some help because now Bob may have rated randomly so Alice and Carol would learn nothing about Bob’s real rating. But even here, if the random raters are assigned and Alice was the assigned random rater (eg ${\textstyle F_{d}=0.333}$ ), then she knows the other raters, particularly Bob, is likely to be honest.

This problem could be solved by randomly assigning the random rater. In the scenario above, if all members of the group “roll a 3-sided die” to see if they are to randomly rate, Alice and Carol wouldn’t know if Bob’s answer was random or not. In such a small sample there’s a good chance this wouldn’t work, but for a large statistically valid group it would. This is essentially the same as the cheating survey we discussed last time where students flip two coins to decide if they answer honestly. Of course, in a large group it becomes ever more unlikely that collusion is taking place anyway.

It seems the best we can do is to mitigate the collusion problem but not eliminate it altogether. After all, if everyone except one person is willing to share all information, it seems difficult to prevent them from isolating that one person’s information. The only remedy is for that person to simply not provide the correct answer.