Trust attenuation and the inadequacy of single-value trust factors
More actions
Main article: Technical overview of the ratings system
One problem, especially for trust networks with multiple levels is trust attenuation. Let’s start by following up on some points that were raised about this:
Why we're not using a tree topology
The examples show a single straight line representing the originating client (top-node) to the server (leaf node) that answers the query. The rest of the tree is simply not shown because the query is difficult and very few nodes, in this case one for simplicity, can answer it. So although a tree is there, most branches start cycling and never break out to a fruitful leaf, time-out, etc. So the topology in this case is modeled as a straight line to the one server node that has information to offer.
Why don't we just have a bigger network?
This is a very similar question. The example above posits a tough question for which there are a limited number of sources. The problem is by definition limited to very few leaf nodes. But let's say we had more than one. In the example shown last week, where P=53% with one server, a two-source (server) problem with the same number of levels leads to P=56%. 3 sources (servers) leads to 59%, etc. Eventually we'll have enough server nodes to overcome the attenuation but until we do, we are generating bad answers. Meanwhile the attenuation could easily be worse than this example suggests. We could have a situation that's so attenuated that you have, say, P=50.5% combined probability. It will take many independent sources of information to overcome this.
A bigger network is a reasonable solution only if we're sure it will be big enough to overwhelm the attenuation effect. For an easy question, this is probably a safe bet -- thousands of server nodes with real information will dominate the low-integer number of levels in our network. But I don't think we can count on that for a hard question, one that's about a single person or a handful of people.
Node Registries as a Potential Solution
A node registry has been proposed to deal, in part, with this problem. This would certainly work to short-circuit the path from the originating client to the server and eliminate the issue of trust attenuation. Of course it leaves open the issue of how to establish trust with an unknown node, but this could be handled in various ways: if available, average the trust factors of the server node's immediate contacts, simply allow the client to determine their own level of trust over time, etc.
The inadequacy of single-value trust factors
Node registries will work but we still have the problem of attenuation in the regular network. So, for that network, let's note that this whole conversation is predicated on the idea that there is something fundamentally wrong with allowing answers to wash out just because of the trust factors of otherwise neutral nodes -- nodes that really do nothing more than pass information along.
This leads us to the notion that using the same trust factor to pass information as we use to provide information is wrong in general. Trust is essentially a way to correct for a node making a mistake -- presumably in answering a real question using its own judgement. This is quite different than a node that is simply reporting an answer from other nodes, a process which is (or should be) largely automatic. It would seem that, at the very least, we would need two trust factors, one for providing answers and another to pass answers along. In our case, one where each node is both providing and passing, we'd need to modify the Bayes Eqn with Trust (https://ceur-ws.org/Vol-1664/w9.pdf) to include both trust factors. One would be the trust on the node's personal opinion and another on the opinion it gets from its child. Presumably the child-based opinion will be passed along with a much higher trust factor.
Doing this reduces trust attenuation but does not entirely remove it. The remaining attenuation will now, however, be based on a reasonable interpretation of trust, that is the trust we have solely in the communication of results. The fact that attenuation "error" will build up as we traverse the nodes up the tree is also a reasonable, if regrettable, phenomenon. Simplistically, if I trust that my child is reporting correctly 80% of the time and it trusts its child 80%, I then have a 0.8*0.8=64% chance of getting the correct report from the child's child. Attenuation still happens but at least it's understood and does not represent an error.
Example
Let's look at an example:
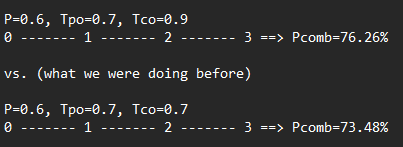
If we have 4 nodes, and we differentiate between the personal opinion trust (Tpo) and communication trust (Tco) where Tpo=0.7 and Tco=0.9, we obtain a Pcomb=76.26% whereas we obtain Pcomb=73.48% if Tpo=Tco=0.7 (same as using a single trust factor). This is a modest, although significant, improvement. A detailed example of how this calculation was done is located here.
For 8 nodes the difference, as expected, is greater:

Script to do calculations
Also a snippet: https://gitlab.syncad.com/peerverity/trust-model-playground/-/snippets/130
'''sapienza_trustline.py
Rolls up Probability for a single line, leaf to top-node, using two trust factors: personal opinion and communication.
eg
P=0.6, Tpo=0.7, Tco=0.7
0 ------- 1 ------- 2 ------- 3 ==> Pcomb=73.48%
P=0.6, Tpo=0.7, Tco=0.9
0 ------- 1 ------- 2 ------- 3 ==> Pcomb=76.26%
'''
import numpy as np
#from sapienza_bayes.py, based on paper by Sapienza -- https://ceur-ws.org/Vol-1664/w9.pdf
#Also reproduces the app -- https://peerverity.pages.syncad.com/trust-model-playground/
# Calculates the combined probability given a vector of Probabilities and Trust.
def calcpc(P,T):
Nchoices = len(P[0])
Pnom = 1.0/Nchoices
P = Pnom + (P - Pnom)*T
Pcomb = np.prod(P,axis=0)/sum(np.prod(P,axis=0)) #A modified version of Bayes eqn given in paper as f(P|E) = f(E|P)*f(P)/f(E)
return Pcomb
#start example
numnodes = 4 #0,1,2,3
Ppo = [0.6] * numnodes
# po co (personal opinion trust, communication trust)
Toc = [[1.0,1.0]] + [[0.7,0.7]]*(numnodes - 1)
#OR type in each one separately:
#Ppo = [0.6, 0.6, 0.6, 0.6] #personal opinion probabilities for nodes 0-3
#Toc = [[1.0,1.0], [0.7,0.9], [0.7,0.9], [0.7,0.9]] #trusts for opinion, o, and communication, c -- nodes 0-3 (node 0 is 1.0,1.0 because it trusts itself)
Pcomblast = [0.5, 0.5] #last node doesn't have computed (ie combined) probabilities, so we just assign it to neutral to make calcs consistent
assert len(Ppo) == len(Toc), 'Length of Ppo and Toc must be the same'
assert Toc[0] == [1.0, 1.0], 'The top node should trust itself, ie Toc[0]=(1.0,1.0)'
assert Pcomblast == [0.5, 0.5], 'The last node should have neutral probability, ie [0.5, 0.5]'
#numnodes = len(Ppo)
#Inefficient but preallocate the lists we'll need so we don't have to reverse and append which is clumsy
P = list(range(numnodes))
T = list(range(numnodes))
Pcomb = list(range(numnodes))
i = len(P) - 1
#start with the bottom node and work up
while(i >= 0):
if(i == (len(P) - 1)):
P[i] = np.array([ [Ppo[i], 1.-Ppo[i]], Pcomblast])
else:
P[i] = np.array([ [Ppo[i], (1.-Ppo[i])], Pcomb[i+1] ])
T[i] = np.array([ [Toc[i][0]], [Toc[i][1]] ])
Pcomb[i] = calcpc(P[i], T[i])
print('Pcomb[i], i = ', Pcomb[i], i)
i = i - 1
Detailed calculations
I thought it might be useful to document the calculations, step by step, behind the two-trust factors, as described above. A python script which does these calculations is located here.
This is strictly optional reading or if you just like getting into the weeds.
Let’s start with the example shown, the 4 nodes where Ppo=0.6, Tpo=0.7 and Tco=0.9. Node 0 is the top-node, the client asking the question. Some definitions:
- Ppo = Probability of personal opinion being true
- Pco = Probability of communicated opinion being true
- Pcomb = Combined probability for Ppo and Pco using Bayes’ eqn.
- Tpo = Trust in personal opinion
- Tco = Trust in communicated opinion
- Pnom = Nominal probability for a predicate type question = 0.5
Note that the Pco for most of the nodes is unknown at this point, because it needs to be calculated starting with the last node (3). For node 3, Pco=0.5 meaning that there is no communicated opinion from the next lower node, because a next lower node doesn’t exist. Saying Pco=0.5 is just a way to enter a neutral number, one that won’t affect the calculation.
So we start with the last node and work our way up. Our objective is to find Pco for each node, until we get to Node 0. The Node 0 Pco will then be combined with the Node 0 Ppo to create a final probability, Pcomb (using Bayes’ eqn).
Find Pco for Node 2
Pco for node 2 is calculated by adjusting Ppo and Pco for node 3 by the trust factors Tpo and Tco (for the 2-3 connection) using Sapienza's equation and then combining them using Bayes' eqn (https://ceur-ws.org/Vol-1664/w9.pdf):
Note that has no impact on the calculation. P=0.5 is completely neutral, either for trust adjustments based on Sapienza’s equation or in Bayes’ eqn.
Now that we’ve calculated the Pco for Node 2, we can fill in this information in the diagram:
Find Pco for Node 1
We use the same approach as above, except with the Node 2 P values and connection 1-2 T values:
We can now fill in the Pco for Node 1 on the diagram:
Find Pco for Node 0
We use the same approach as above, except with the Node 1 P values and connection 0-1 T values:
We can now fill in the Pco for Node 0 on the diagram:
Find Pcomb for Node 0
All that is left to do is calculate the combined probability for Node 0, which is the final answer. Since Node 0 trusts itself we do not need to adjust the probabilities using the trust equation.
Note that we could have found the Pcomb for Nodes 1,2,3 as well using this equation but didn’t do it because we’re mainly concerned with Node 0. Now we can present a complete diagram with the final answer: