More actions
Main article: Money system based on ratings
Main article: Political systems
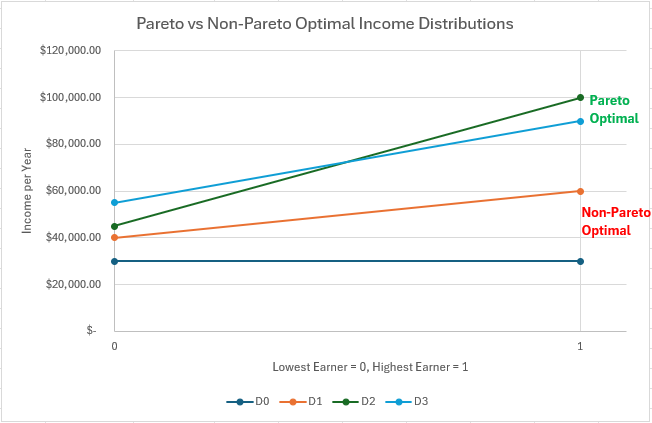
Communities may choose to set rules or norms for income distribution in an attempt to maximize some metric of societal good. These may result in a more or less equal income distribution than the one western capitalism yields. But how would we define an optimal distribution? A starting point for deciding this could start with a condition of Pareto optimality. That is, we stipulate that a Pareto sub-optimal distribution is one in which everyone is worse off. The figure below shows several simplified distributions. We reject the two curves on the bottom because everyone is worse off if they are chosen. The two curves at the top represent Pareto optimality. Here we are improving the welfare of some members at the expense of others. We would need another figure of merit, or a subjective judgement, to decide which of these Pareto-optimal distributions is actually the best.
We might choose to maximize total income or HDI as our figure of merit. We could choose to impose an income floor (or HDI floor) and then choose an income maximization scheme for those distributions above the floor. This would ensure that everyone meets a minimum standard of living but, beyond that, we can allow a more laissez faire policy to govern. A variety of other schemes might be envisioned which communities could decide on.
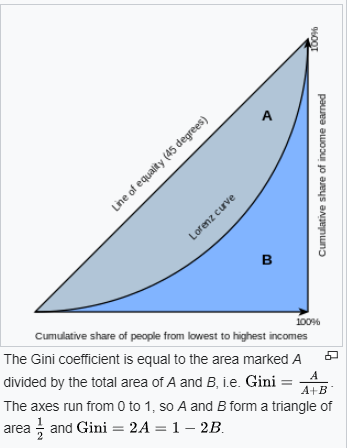
The main metric used to measure income inequality is the Gini coefficient, named for the Italian statistician Corrado Gini. It is a number between 0 and 1 where 0 represents perfect equality and 1 represents perfect inequality. It is most intuitively calculated by plotting the actual income distribution in a society along with the equal income distribution:
Source: https://en.wikipedia.org/wiki/Gini_coefficient
The Gini coefficient is area A divided by A+B. Note that societies with a completely equal distribution have a straight 45 degree line since any percentage segment of society, say the first 25%, receive 25% of its income. The actual distribution is called a Lorenz curve (for the US economist Max Lorenz) which, for unequal societies, is always under the equality curve. This means, using the same example, that the bottom 25% of society makes less than 25% of the income. A Gini coefficient of 1 means that one person is receiving all the income in society and the rest gets nothing. This would be a horizontal Lorenz curve (at 0) which extends all the way to nearly 100% (the last, richest, person) and then shoots up to 100% income.
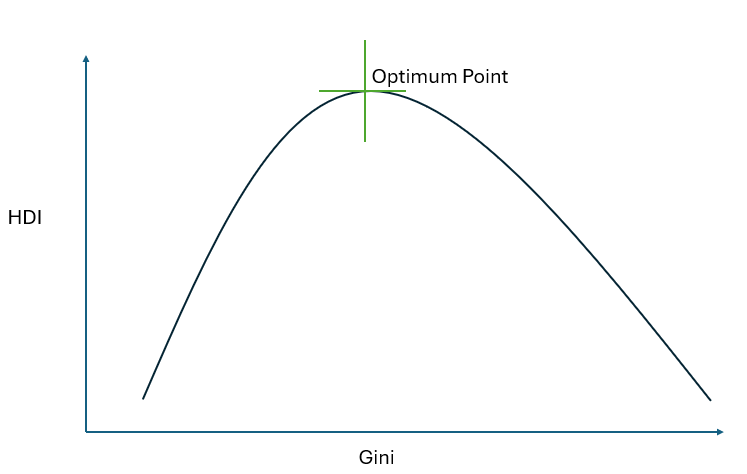
If we use the Gini coefficient, which seems reasonable, our optimization problem would amount to maximizing HDI as a function of Gini coefficient.
– This gives Gini at maximum HDI point
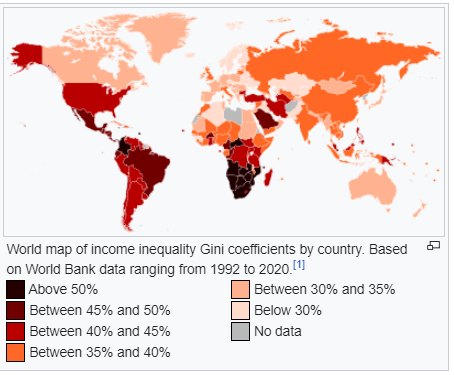
Here is a map of the world colored by Gini coefficient:
Source: https://en.wikipedia.org/wiki/List_of_countries_by_income_equality
While we’re at it, let’s discuss the Marxist notion of income distribution which is that everyone receives what they need. This may have seemed reasonable to Marx since he wrote in the days before widespread social insurance programs. But today we can expect, especially for a planned society, that social insurance programs will handle needs that go beyond that of the typical healthy worker: medical care for the sick, income replacement for the elderly/disabled, etc. In addition we can expect, as a post-scarcity society, that food will be plentiful enough for everyone. It would be ridiculous to think that someone with a high metabolism (who thus needs more food) would go hungry compared to someone with a lower metabolism. Similarly, for education, those willing and able would be expected to have access to the learning resources they need. With these ideas in place, we have probably satisfied Marx’s concern with need. This leaves us with an equal income distribution, one that is probably not optimal since it does not provide any economic incentive to improve. In other words, we can presumably find an alternative to a Marxist distribution which raises everyone’s income.
In terms of our contemporary society, let's touch on a few methods to modify income distribution. The most common, as mentioned, is social insurance programs which provide supplemental income to the elderly, state-sponsored medical insurance, subsidized education (eg public schools), public infrastructure (eg parks, roads), food stamps, etc. More avant garde ideas include universal basic income (UBI) in which everyone receives a fixed income. The program is available to everyone so as to avoid the administrative overhead associated with traditional welfare programs. Another idea that has been tried in many forms is to modify taxation levels to favor those lower in income (graduated income tax, tax credits, etc).
One idea on this front is the philosophy of Ingrid Robeyns, a Dutch academic, who favors Limitarianism, a society in which excess wealth is limited. Her view is that extreme wealth accumulation is unethical and bad for society. She favors a straightforward wealth tax which would keep anyone from exceeding $10 M in net worth. She does not have a political idea, other than conventional organizing, about how to achieve this goal. This is a common problem with reasonable ideas that fly in the face of convention.