More actions
Main article: System modeling
This section primarily addresses the PAPRIKA method by 1000minds.com.
One of our challenges will be creating decision making algorithms that are simple for most users. One such method is called PAPRIKA (Potentially All Pairwise Rankings of all Possible Alternatives). This method makes it very easy to compare alternatives by ranking desirable characteristics. For example the two criteria for a job candidate might be education and experience. The two levels would be high and low, so we would have all combinations of high education, low education, high experience, and low experience. Clearly we can eliminate candidates with low education and low experience. Let’s further assume that candidates with high education and high experience are not available since their presence obviates the need to make a choice at all. All other categories involve the choice between high education, low experience vs low education, high experience. The decision is therefore in how much education vs. experience matters. This can be settled by simply asking the question, “what is more important, education or experience?”. By asking simple pairwise questions the method is able to rank any possible set of choices. It claims to be the easiest decision algorithm for ordinary people because of the simplicity of the interrogation method.
PAPRIKA was used originally to generate patient-tailored care approaches for people with arthritis. In essence, the system gets the patient to choose the type of treatment they prefer given its efficacy, side-effects, risks, etc.
MCDM methods are concerned with extracting preference information because of the inevitable presence of non-dominated sets of choices in all but the most trivial problems. A dominated choice is one for which a clearly better alternative exists. A job candidate with low experience and high education is always dominated by the one with high experience and high education. Non-dominated simply refers to sets of choices which have no clearly better alternative (high education, low experience / low education, high experience) and which thus require a choice.
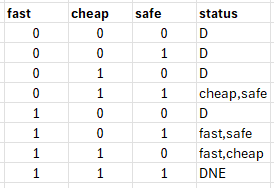
For example, you might want a car that is fast, cheap, and safe. Let’s suppose that, at best, you can have only two of the three (ie the fast, cheap, and safe car does not exist). Let’s further suppose that there are only two quality levels in each category, that is the car is either fast or slow, cheap or expensive, and safe or unsafe. We can then construct a table of all possible options:
The DNE entry is the one that does not exist. The D entries stand for “dominated”, that is, for every one of them, there is an objectively better alternative so no rational decision maker would ever choose them.
This leaves us with three non-dominated options, as shown in the table.
- slow, cheap, safe
- fast, expensive, safe
- fast, cheap, unsafe
The choice is between (cheap, safe), (fast, safe) and (fast, cheap). We could ask the user to simply rank order their preferences from 1 to 3 of the three quality attributes. Suppose the user had answered:
- fast
- cheap
- safe
Now we know that the (fast, cheap) option is best for this user since he obviously prioritizes safety the least. But in a long list of options this might be difficult, so an alternative way to ask for the same information would be to break down the questions:
- Do you prefer faster or cheaper? A: Faster
- Do you prefer cheaper or safer? A: Cheaper
It is easier to answer these two simple questions than it is to rank order the list from scratch (this is easier to see for longer lists). Indeed, these answers can be used to generate the exact same rank ordering that we had above. Both methods lead us to the fast and cheap alternative.
PAPRIKAs algorithm works for long lists of choices by eliminating dominated choices, identifying implicitly ranked pairs, and removing non-unique choices. For example, a system with 8 criteria and 4 categories within each leads to 65,536 possible alternatives (4**8) and which requires 95 pairwise ranking questions.
MCDM has the disadvantage of having an exponentially increasing set of alternatives as the number of criteria increases. We will have to watch that and ensure that we develop algorithms that are computationally tractable.
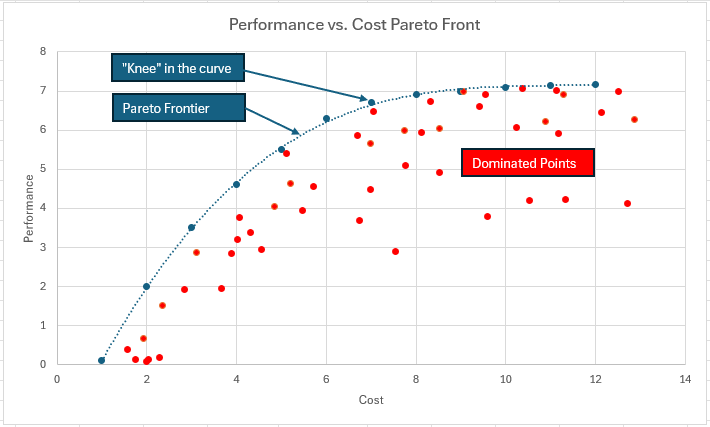
One generic way to present multi-criteria decision options is in terms of a Pareto front, which often looks like the following:
Here we plot generic Performance vs. Cost of several system designs (eg a satellite) and our goal is to choose an optimum configuration. The best performance for the cost is obtained by picking designs on the Pareto frontier. All other points (the red ones) are dominated by the Pareto front and there would be no reason to choose them.
Within the subset of points on the Pareto front the decision of which one to pick is subjective. What is the budget for the project? Is there a minimum level of Performance required? Graphs like these frequently have a “knee in the curve” which indicates a point of diminishing returns, that is beyond which only a small amount of performance improvement can be had at great cost.
Engineering software at the system level is generally able to produce this type of chart, frequently the result of a genetic algorithm for optimization, which takes into account multiple objectives. Also important is the ability to roll-up an overall Performance metric which is often composed of various criteria. In a satellite it might be energy efficiency, coverage, image quality, etc. Sometimes the performance metric is known as a figure of merit and is the result of a somewhat subjective weighting equation. Our system will be able to establish equations of this type through its consensus mechanisms.
Our information network may not be interested in systems engineering but the ability to do this type of analysis is useful for consumers as well. Consider that sales is often an effort to increase the consumer’s cost without adding much value. It is an attempt to convince you to buy somewhere on the flat part of the Pareto curve or perhaps even in the dominated space.