More actions
Main article: Technical overview of the ratings system
This discussion will show how cycling in trust networks rapidly leads to an incorrect answer (Pcomb) which is often much higher than the answer you would get in a non-cycling network. The divergence between answers, however, depends on trust. If trust is low the answers will tend to converge and will be equal when trust is zero. If trust is high the answers will be very far apart.
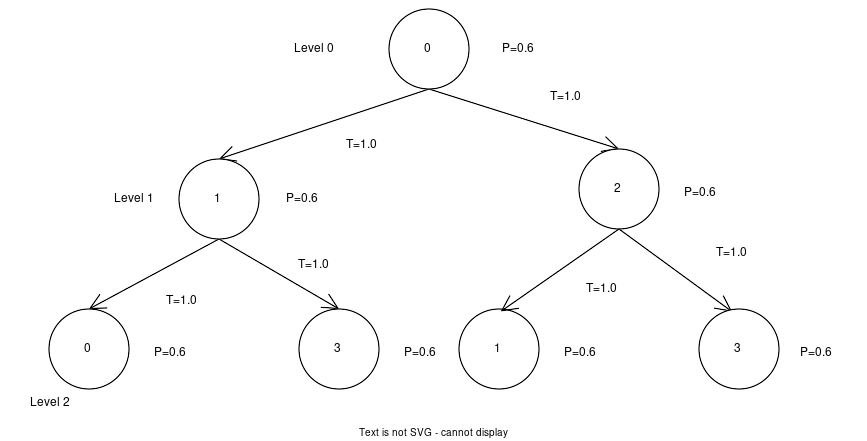
Suppose we have a trust network composed of four Nodes 0, 1, 2, 3 with the following connectivity: {0:[1,2], 1:[0,3], 2:[0,3], 3:[0,1]}. That is, Node 0 is connected to Nodes 1 and 2, Node 1 is connected to Nodes 0 and 3, etc.
Each node has the following probabilities which we will say are all the same for the sake of simplicity: [0.6, 0.4], [0.6, 0.4], [0.6, 0.4], [0.6, 0.4]. That is, Node 0 is 60% confident in its prediction, Node 1 is 60% confident in its prediction, etc.
We will restrict ourselves for now to the case where Trust is 1.0. We will do a case later where the trust is below 1.
This situation looks like the following if we have three “levels” (0-2) and is clearly cycling since Nodes 0, 1, and 3 are used more than once.
Node 0 will try to answer a predicate type question, such as “will it rain tomorrow, yes or no?”. It has its own confidence of 60% and has friends 1 and 2 who also have 60% confidence in their prediction. They in turn have their friends on Level 2 who are 60% confident in their prediction.
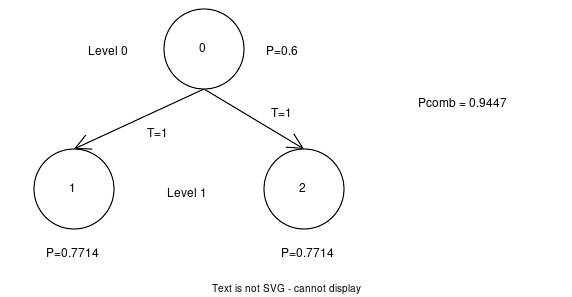
We can calculate this by starting at the bottom-most level (Level 2) which requires no calculation and just defaults to each node’s own confidence (ie 60%). Then we can combine that with the next higher level using Eric’s app (https://peerverity.pages.syncad.com/trust-model-playground/) or the scriptsapienza_bayes2. So, the nodes 1, 0, and 3 all have probabilities of 60% and will combine to create a probability of 0.7714. Similarly the nodes 2, 1, and 3 will combine to create a probability of 0.7714. We now have the following situation:
We can continue with Eric’s app or sapienza_bayes2.py to roll up the combined probability of Node 0, 1, and 2 which turns out to be 0.9447.
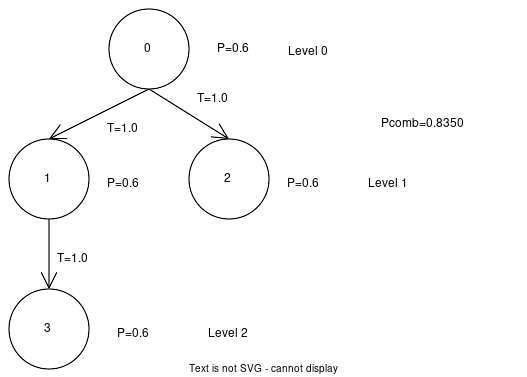
The same non-cycling network looks like this and has a combined probability of 0.8350:
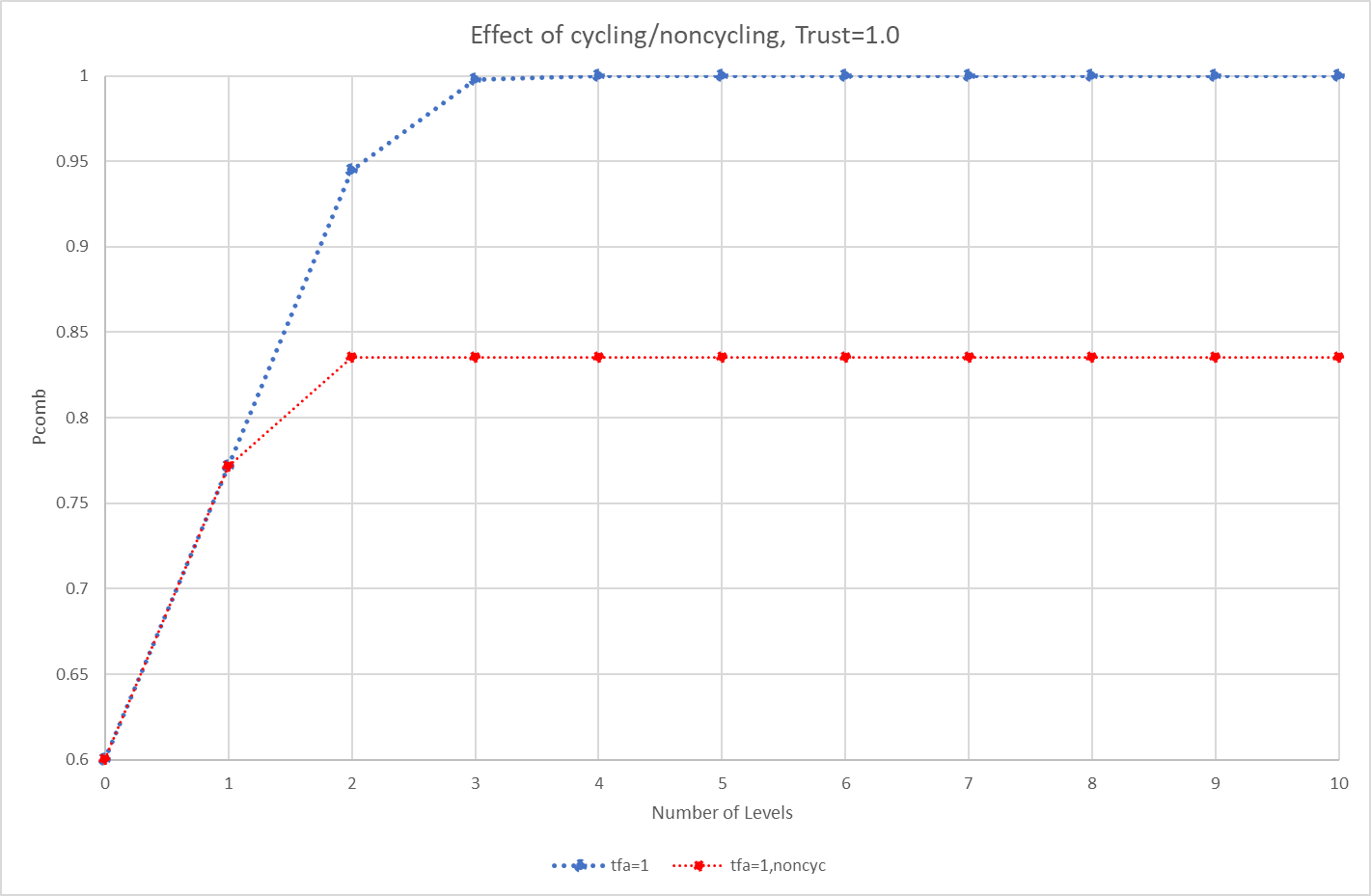
The non-cycling network uses each node only once and yields a significantly lower Pcomb than the cycling network. And this is only for a 3-level network. We suspect that continuing to add levels which cycle will quickly lead to a confidence of 100% (or 0% if the probabilities were under 50%). Indeed if we added just one additional level to this example (Level 3), Pcomb = 0.9977.
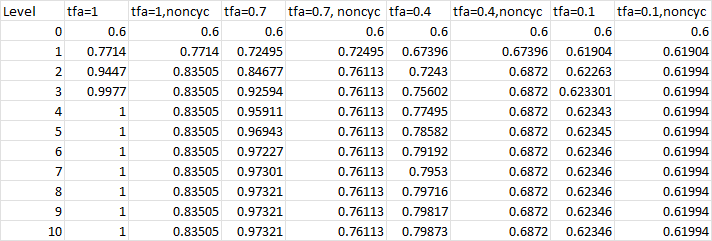
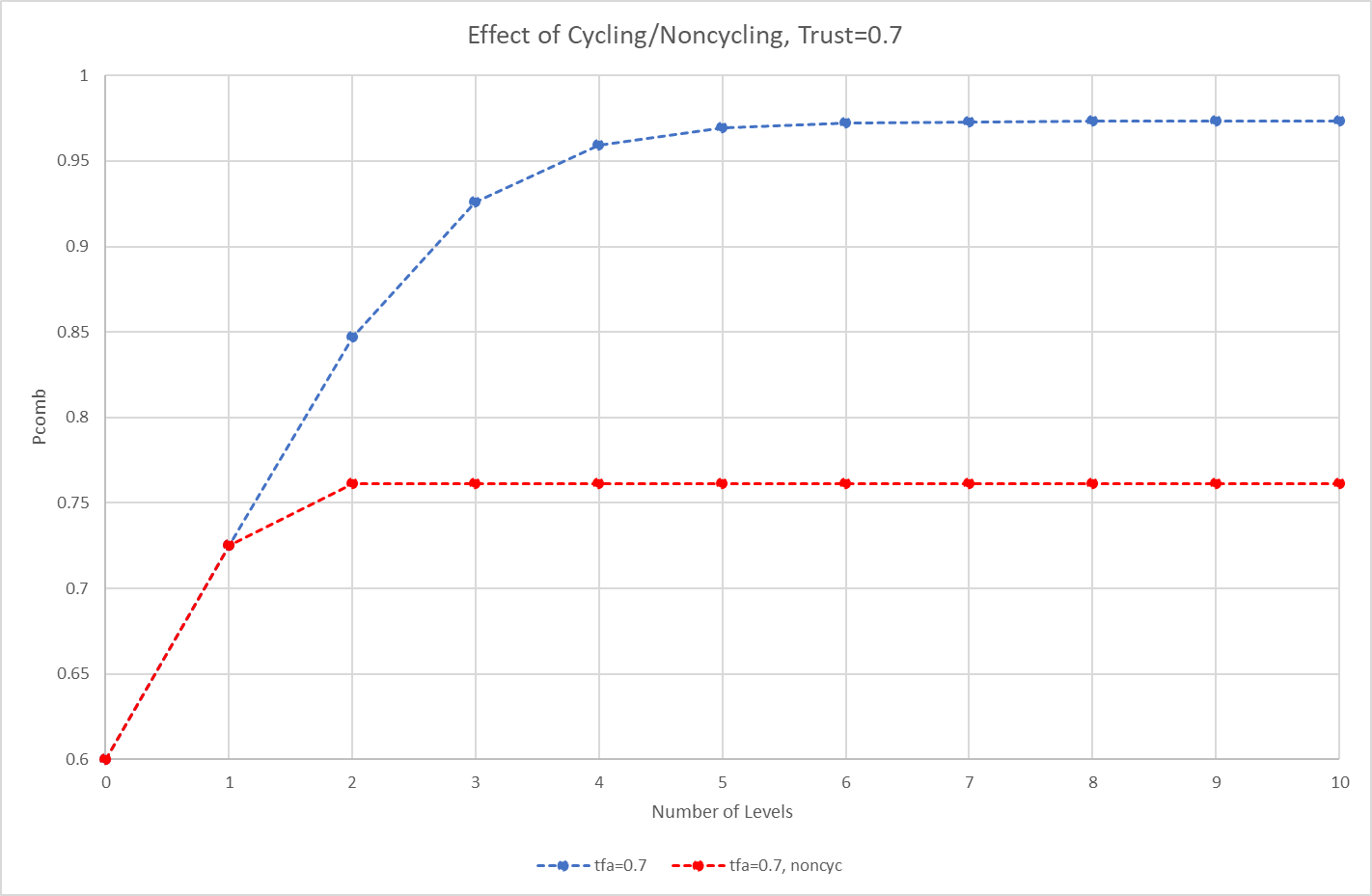
Adding in trust factors below 1 will mitigate this effect to some extent but the overall divergence between cycling and non-cycling will still be obvious unless the trust is very low. For instance, repeating the above calculations with Trust=0.7 between all parties leads to Pcomb = 0.97 for the cycling case after 6 levels and Pcomb = 0.76 after 3 levels. Interestingly, the Pcomb does not approach 1.0 in the limit of many levels like it does for Trust=1. Instead it approaches an asymptotic limit which depends on the trust and becomes lower as the trust becomes lower.
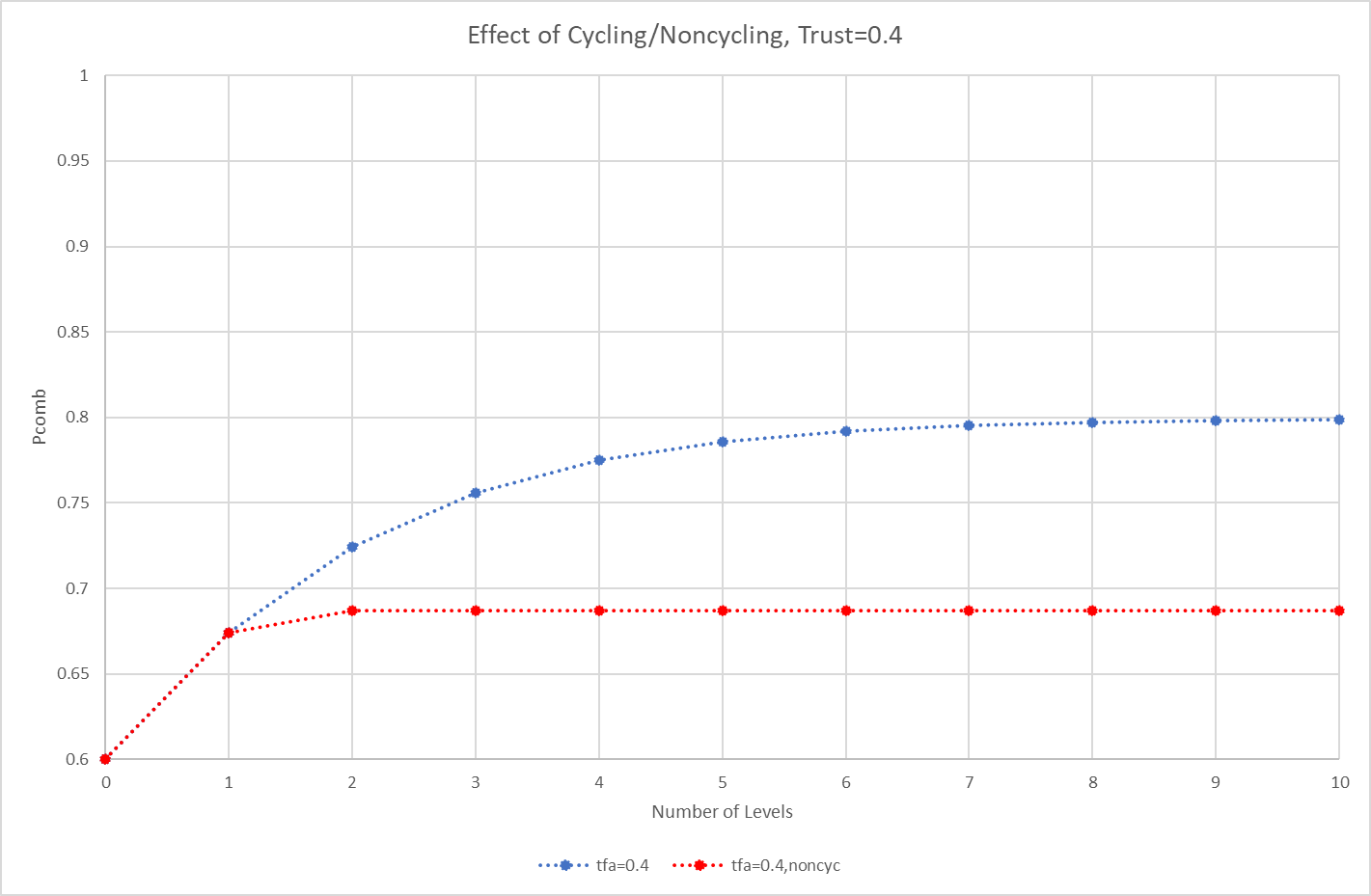
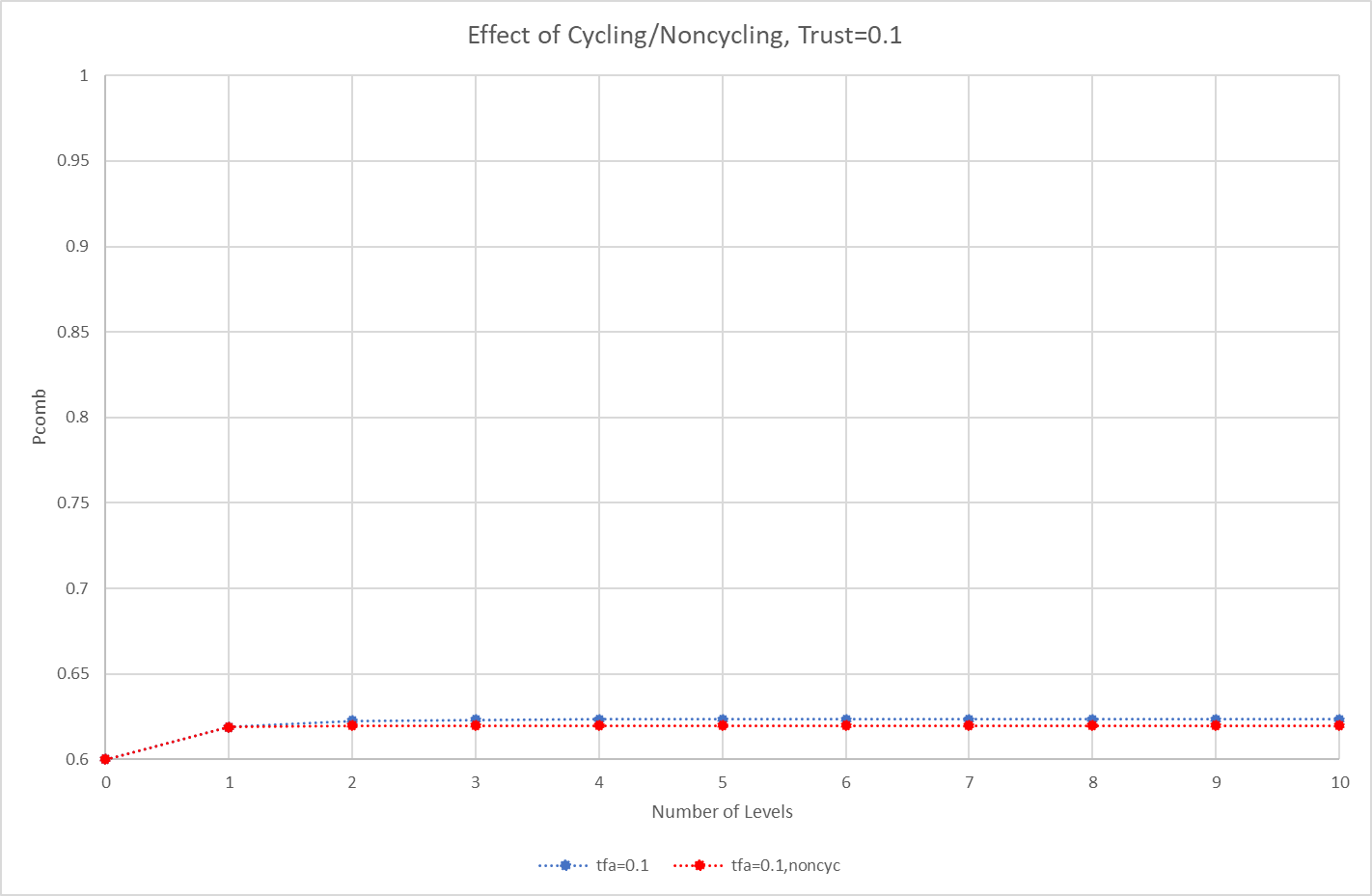
The following table illustrates this situation for the case of Trust, ie tfa (trust for all) = 1.0, 0.7, 0.4, and 0.1. For Trust = 0, the Pcomb values will remain at 0.6 since all nodes will be “neutral” except for the top-most node (Node 0) which will use its own default confidence of 0.6 (and implicitly trusts itself, ie Trust=1.0). The trust calculations are taken directly from the Sapienza paper, ( https://ceur-ws.org/Vol-1664/w9.pdf ). Here’s a Python script to do the calculations, based on the paper, which allows us to create a network and roll up the probabilities into a single Pcomb, with cycling and without: sapienza_trusttree
Here are some plots of the above: