Deductive & inductive arguments and use cases

Main article: Logic

Deductive Arguments and Use Cases

Deductive arguments are ones where the conclusion must be true if the premises are true. They can be reduced to symbolic form and proven in the same way that we prove math theorems. They aren’t as common as inductive arguments (more on those later) but they form the foundation for all arguments and have significant applications of their own.

Let’s take an example of a deductive argument that might be used in a real debate about cryptocurrency:

1. When government agencies control entire sectors of the economy, it leads to worse economic performance than if private enterprise is involved.
2. The Federal Reserve controls the entirety of the money supply in the US.
3. The Federal Reserve is, for all practical purposes, a government agency.
4. The money supply can be considered an entire sector of the economy.
5. Therefore it would be better for the economy if private enterprise were involved in creating our money.
6. Cryptocurrency is a private way to create money.
7. Conclusion: It is better for the economy if cryptocurrency were involved in our money creation.

This argument is straightforward and, like all deductive arguments, foolproof if we accept the premises. Doubts about the premises would likely center on 2 and 3. Is the money supply really a “sector” of the economy as we understand it from premise 1? Does the Federal Reserve really control it entirely?, and so on. These are no doubt points that would be debated by those who feel strongly about this issue. Nevertheless, accepting the premises, we have no choice but to accept the conclusion.

Philosophical Arguments

Let’s take a look at an argument for reincarnation, broken into a few simple deductive sub-arguments:

1. Before I existed, the universe held a finite probability of my existence in any given place and time. I know this because I now exist.
2. My existence does not significantly change the universe’s probability that I might exist again.
3. Therefore, when I die (stop existing) the universe will again contain about the same finite probability of my existence in a given place and time that it had before.
4. This probability increases with the size of the domain in which I could exist again, up to the limit of 100%.
5. Therefore, if the universe is infinite the probability that I will exist again is, in the limit, 100%.
6. The universe is really infinite despite what is considered the size of our “observable universe”.
7. Final Conclusion: Therefore the chance that I will exist again is effectively 100%.

This argument has an obvious weakness in one of its premises, that of an infinite universe. If the universe is not really infinite, at least in terms of events that we are interested in, it becomes much weaker. But accepting this premise, and the others, one can accept the conclusion. Let me just say that this argument is quite effective. Many people take the premises and conclusion seriously, whether they ultimately “believe in” reincarnation or not. It is an example of pure deductive reasoning and its deductive nature makes it more compelling since if you accept the premises, you have no choice but to accept the conclusion.

Many philosophical arguments work this way. They reason from a set of premises which are hard or tricky to dispute and come to an irrevocable conclusion. Kurt Godel published a proof for the existence of God which was shown by an automatic proof checker to be algorithmically correct (https://www.scientificamerican.com/article/can-god-be-proved-mathematically/). Again, the only way to dispute his conclusion was to question the premises.

Many arguments try to convince their audience of the truth of a conclusion. However, many have a lower standard which is merely to convince the listener that one side is better than the other. They argue not that A is true and B is not but that it is more reasonable to believe A than B. One stark example of this is Pascal’s wager (https://en.wikipedia.org/wiki/Pascal%27s_wager), summarized here:

1. Either God exists or does not.
2. If God exists and you believe it, then you end up in paradise.
3. If God exists and you don’t believe it, you end up in hell.
4. If God does not exist, nothing happens.
5. Therefore if you believe in God either you will end up in paradise or nothing happens.
6. If you do not believe in God either you will end up in hell or nothing happens.

Either way it is more reasonable to believe that God exists. Some may claim that this is not really an argument at all but a method to scare or bribe people into belief. But even if it leaves the path of sincere faith unstated, it allows the listener to make a decision. With a few more sentences we could then turn this into a foolproof deductive argument. It is one that to this day is deployed by real people (despite the weakness of premises 2 & 3).

Implicit and Practical Uses of Deductive Logic

Deductive logic is often used in implicit ways. Take the following example:

John claims, in Sally’s presence, to be a lawyer but knows nothing about the LSAT. Sally concludes that since John is failing her basic chain of deduction, he is probably not a lawyer.

That deductive chain is:

1. Anyone who gets into law school must take the LSAT.
2. Anyone who is a lawyer must first go to law school.
3. John is a lawyer.
4. Therefore John took the LSAT.

To foreclose the possibility that John simply forgot about the LSAT we could add the premise “No one who takes the LSAT forgets the experience”. Sally now has a robust deductive argument, useful for casting suspicion on John’s claim. Sally’s argument may never actually come to light since people tend to avoid conflict. But she implicitly uses her deduction to reach a conclusion about John.

But if Sally were to confront John she might well have to spell out her deductive reasoning. In that case the argument would likely end up not have anything to do with the logic of the deduction itself which, in this case, is foolproof. It would, as usual, center on the premises Sally made. John might argue, for instance, that the law school he went to was an exception and didn’t require the LSAT. Or that in his jurisdiction he can become a lawyer without attending law school. But now the conflict between Sally and John rests on a matter of fact, not reasoning, and can be challenged on its own terms.

Deductive arguments often come to light when it is necessary to resolve a dispute, such as in a court case, a business negotiation, etc. They make their appearance when the stakes are high and a resolution is necessary.

A political/public policy argument

They also come out in debates about public policy. Let’s take a look at a current and fairly standard type of argument in this vein:

Since inflation is low and unemployment is low and the economy is growing robustly, the economy is doing well. Most voters, however, think the economy is doing badly. Therefore most voters are either misinformed, answering dishonestly, or misunderstand the question.

Laid out as a deductive argument, this might be stated as:

1. If inflation is low, unemployment is low, and the economy is growing robustly, it is doing well.
2. Inflation is low, unemployment is low, and the economy is growing robustly.
3. Therefore, it is a fact that the economy is doing well.
4. People who negate facts are wrong.
5. If someone is wrong about something it is because they are misinformed, answering dishonestly, or misunderstand the question.
6. Most voters negate the fact that the economy is doing well.
7. Therefore most voters are misinformed, answering dishonestly, or misunderstand the question.

This argument is featured, in one form or another, in the news these days and is based on survey results. Again, its power rests on premises and, especially in this case, definitions. Above, we more or less defined what the economy means in the context of doing well or poorly. We focused on macro inflation indicators, unemployment, and growth. But an individual voter might think the economy means gas prices or whether his kids can find good jobs. He might also disagree, quite reasonably, with how low inflation or unemployment have to be to be considered “good”. If the respondent does not share a common definition, then the entire argument is flawed.

Opinion surveys are notorious for asking questions incorrectly and getting skewed results. And it is normal for arguments to be enthymemes, ones where premises (or even conclusions) are not explicitly stated. Deductive arguments need to be careful to define their terms up front, within the premises, and not skip steps.

Definitions

Terms like “the economy” and “infinity” are tricky because we believe we know what they mean but often we don’t. Concepts like “God” are generally vague and subject to personal interpretation (ie he can send you to hell or paradise). Users of deductive logic often use these terms to gain traction with their arguments, glossing over complex definitions in the hope that they will gain acceptance for their point of view. Precise definitions are an important ingredient in any real system of logical analysis. A logic analyzer should be able to identify incomplete arguments that result from ignoring definitions.

Even when precise definitions are readily available, a motivated debater can still try to confuse the meanings of terms by practically redefining them in the premises:

1. Anyone who is anti-zionist is anti-semitic.
2. Bill is anti-zionist.
3. Therefore Bill is anti-semitic.

Inductive Arguments and Use Cases

Let’s start transitioning into inductive arguments. Unlike deductive arguments, whose conclusion is irrefutable given the premises, an inductive argument is one where the conclusion is only likely given the premises. Most reasoning in the real world is inductive, although deduction often underlies it.

Argument from Analogy

Let’s take one very common form of induction, the argument by analogy:

1. Jim took his Ford to Paul’s repair shop 5 times and got good results.
2. Jim took his Nissan to Paul’s repair shop 8 times and got good results.
3. Jim took his Volkswagen to Paul’s repair shop 6 times and got good results.
4. Therefore Jim will take his Tesla to Paul’s repair shop and expects good results.

Because Jim has had all good results with Paul with different makes of vehicle, he believes he will always get good results with Paul. Jim may be implicitly using the following deductive logic:

1. Paul’s repair work for any car is always good.
2. Therefore, Paul’s repair work for my Tesla will be good.

Obviously step 1 in the deduction above is not necessarily true from the evidence presented, but people frequently make generalizations like this. Generalizations turn out to be a legitimate part of inductive analysis. Arguments from analogy obviously raise questions about the quality of the evidence. The more vehicle types that Paul is experienced with increases the quality but if he doesn’t have any experience with electric vehicles, that decreases it.

Inductive arguments can usually only be rated in comparison to each other. Unfortunately, there is no automatic way to determine the quality of an inductive argument. Let’s suppose someone else, John, has used Paul’s repair shop a hundred times with more makes of vehicle than Jim. But he only gets good results 75% of the time. We would likely side with John’s assessment of Paul’s repair shop. This might seem like a straightforward comparison but let’s say a third customer, Joan, has taken her Tesla to Paul 5 times and has a 100% success rate. Her evidence is more relevant because Jim has a Tesla but she’s only used Paul’s shop a small number of times. Rating the merits of inductive arguments can quickly become difficult.

Arguments from induction, and especially arguments by analogy, rely heavily on the relevance of the evidence. The color of Jim’s car is irrelevant to Paul’s ability to repair it. The weather is probably irrelevant too but you might envision scenarios where this is a factor. Relevance is often a sliding scale and is difficult to pin down.

Inductive arguments are often used in science and law. If we observe the attraction between a magnet and iron a number of times, we conclude that it will happen every time. All experimentally derived conclusions ultimately work this way. In common law decisions are based on analogous cases of the past. Court cases can amount to deciding whether one lawyer’s analogy is better than his opponent’s.

Probability in Inductive Reasoning

As you might expect, probabilistic analysis is a large component of inductive arguments, especially scientific ones. Suppose a controversial new drug has come out that cures disease X. It is controversial because, for some people, it has side effects that are worse than the disease it cures. Taking the drug is therefore more dangerous than just letting the disease run its course with no drug. The argument for the drug might go something like this:

1. Sally has disease X.
2. The new drug cures disease X in 100% of patients.
3. The new drug is more dangerous than the disease it cures in 0.1% of patients.
4. Sally should probably take the drug.

Clearly the argument hinges on the number of patients who get the side effects. But it also hinges on the severity of the disease vs. the side effects. If the disease causes temporary paralysis but the side effects are lifelong paralysis, Sally might think twice about taking the drug.

Note that this inductive argument conceals a deductive argument if we replace the percentages by certainty:

1. Sally has disease X.
2. The new drug cures disease X in 100% of patients.
3. The new drug is more dangerous than the disease it cures in 0% of patients (ie there are no worse side effects).
4. Anyone that has disease X should take a drug that cures it if the drug has no worse side effects than the disease itself.
5. Sally should take the new drug.

We added premise 4 to the argument which is simply an obvious point to create a complete chain of deduction. The purpose of this is only to show that deductive arguments are often easy to make from inductive ones when certainty replaces real probabilities. In that sense, deduction is the foundation of induction.

Argument from Authority

Let’s take a look at another inductive argument type, the argument from authority. Here we argue that something is likely true because an authority figure says it is.

Medical Advice

If my doctor says I need a treatment I am likely to believe her simply because she’s a doctor. If I conclude that she’s a bad doctor my recourse is usually just to find another one. If the new doctor says the same thing I am probably just going to believe her, again because she’s a doctor. I might double check what she says by googling it but my sources are just going to be other doctors at places with an online presence, like the Mayo Clinic.

In some cases, I might attempt to second guess my doctor. A homeopathic doctor, for instance, might recommend a dietary change and claim that it works better than the standard treatment. But I haven’t really stopped appealing to authority. Now the job is to weigh the two sides and see which one seems more credible. In fact, everything I do from this point forward is to weigh the evidence presented by authorities. I know very little of the subject myself.

Climate Change

We mostly use the same argument from authority with climate change. We learn about the subject from news organizations we find credible. They interview scientists who have degrees in applicable fields from credible institutions. The scientists publish in respected journals. They work for respected universities and government labs. They have reputations which they are unlikely to want tarnished. They come from many countries and work in many different organizations.

If we want to dig a little deeper, we can find the articles they publish and learn that temperature recording stations exist around the world that have been tracking data for many years. We can learn about how arctic ice is melting and that sea levels are rising. These locations and experiments seem to check out with other sources, even if we never visit them ourselves. In addition, computational models seem to confirm what the data is saying and predict that we are in danger. We usually can’t check the models ourselves but it seems that the varied number of models from many sources is strong confirmation of their truth.

In short, a circle of authoritative credibility surrounds the belief that climate change is real. Furthermore, starting with our own education, we believe in the scientific process itself. We believe that scientists routinely check each other and that science is self-correcting. In particular we believe that if a scientist were to disprove climate change, that science would eventually adopt this new point of view. We believe the scientific system is fundamentally honest.

We can also compare the evidence for climate change with other established scientific theories. Are we using the same standards of evidence for climate change that we normally apply? On this front, climate change appears to be on solid ground. But, in making this judgement, most of us are again just following what authoritative figures tell us. A vanishingly small number of people actually know climate science well enough to think independently on the subject.

This is a good time to reflect on a point made above, that in many cases the absolute truth of a situation may elude us but we can make a decision based on what is more reasonable to believe. Climate change demands a public policy solution, and hence our attention, because if we do nothing, dire consequences are predicted. Again, of course, it is authoritative figures who are telling us about these consequences. Still, given the authoritative evidence and the consequences, most people will think it more reasonable to believe in climate change than not, especially as a public policy matter.

Those skeptical of climate change, or perhaps human-caused climate change, might argue that inducing fear like this is the same as Pascal’s wager, one that provokes anxiety but doesn’t really convince. But if inducing fear causes a genuine search for the truth then it has served its purpose. After all, some things are truly dangerous and we should know about them.

The skeptics' larger point, however, is that just because authoritative figures say something is true doesn't mean it is. It is a point to be taken seriously since experts have certainly been wrong in the past. Efforts are made to present an alternative view of climate change, to poke holes in arguments for it, etc. Authoritative figures on the skeptical side also exist. So who is right? The lay bystander will probably conclude that in a war of authorities, the majority wins. Another alternative is to simply give up but that is not really a viable choice in a public policy arena. Majority-wins is unsatisfying but it is what arguments from authority usually boil down to.

Climate science and its presentation to the public is full of inductive arguments, not just the argument from authority. We will never be able to prove climate change through deduction. All we can do is obtain the best inductive arguments and proceed with whatever public policy is suggested by them.

Causation and Scientific Hypotheses

Another aspect of climate change concerns causation. In fact, whether or not humans cause climate change is the central controversy here. Inductive logic contains a variety of techniques to establish cause. These include, traditionally, Mill’s Methods (https://en.wikipedia.org/wiki/Mill%27s_Methods) and statistical methods such as analysis of variations (ANOVA). Instead of pursuing these in detail we can summarize that they are all an attempt to separate the significant factors of causation from random variations. And, although the techniques are themselves mathematical, there is no automatic way to assess a cause-and-effect argument.

Closely related to causation is the proof of scientific hypotheses. A hypothesis proposes an explanation and tries to prove/disprove it by establishing the following criteria:

1. Adequacy – Does it fit the facts it was intended to explain? Also, is the explanation accurate?
2. Internal coherence – Are internal components of the explanation interconnected rationally?
3. External consistency – Does it agree with, or at least not contradict, other confirmed knowledge?
4. Fruitfulness – Does it suggest new and useful ideas for study?

In other words, we are faced with another set of largely inductive methods for performing this analysis.

Abductive Arguments

One special form of reasoning is abduction, which is an attempt to find the best possible explanation from a given set of facts. Generally the facts are incomplete and several possible explanations exist. Here we will consider it a form of induction because it is closely related to causation and hypotheses. However it is also thought of as being in its own category, alongside deduction and induction. It is often somewhat of a quick, informal process of doing the best you can with what you have:

The grass is wet. You conclude that it must have rained.

Your gas gauge reads empty even though last time you drove the car it was full. You conclude that your spouse drove it several times in between.

Your doctor sees that you have a fever, sore throat, and body aches. It’s flu season. She concludes you have the flu.

Software for Inductive Arguments

It is hard to imagine how inductive arguments can be analyzed through software. They don’t have the strict symbolic representation that deductive arguments do, let alone systematic analysis techniques that can be automated. There is software that could help with pieces of this such as statistical/visualization software (R, SAS, scipy.stats) machine learning algorithms (https://www.tensorflow.org/), text analysis tools (https://www.nltk.org/), argument mapping software (https://www.reasoninglab.com/rationale/), etc. We could perhaps ask respondents to structure their arguments in a pre-established way and then perform an analysis of evidence for relevance, quantity, and veracity. We could also consider training our own AI model to handle a wide variety of arguments.

Since sources of evidence are generally published we could maintain a list of them and ask our network to evaluate them for credibility. This is no more than using the network in the way we’ve already conceived with an appropriate algorithm (eg trust weighted average).

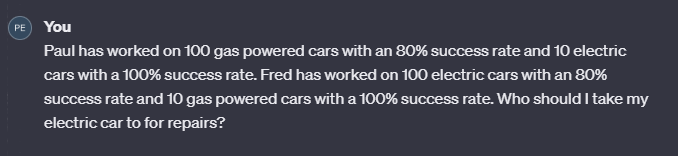
An example of using ChatGPT

To get an idea of ChatGPTs inductive reasoning skills, let’s pose the following problem:

ChatGPT not only fails to understand the crux of the problem but states the answer incorrectly by its own methodology. It states that “for electric cars, Fred has a higher success rate (80%) than Paul (100%)” which is simply wrong. What it probably meant to say was that since Fred has successfully worked on 80 electric cars, and Paul only 10, that Fred is the better choice. It seems to have confused gross numbers with percentage rates. And, needless to say, it continues to be incapable of checking itself in math (80% > 100% ?).

Of course what we wanted it to do was to understand that although Paul’s percentage is higher he has worked on fewer electric cars than Fred. A reasonable method might have assigned a weight to experience and another weight to percent success and calculated it that way. In so doing, it might also have acknowledged that 10 cars is not a great statistical sample and that 100 is better. It also would have taken into account the overall success of both mechanics with all types of cars, something which in this case is equal, but nonetheless should be noted and perhaps entered as part of a weighting equation. ChatGPT does none of this.