More actions
Created page with "{{Main|System modeling}} We have discussed optimization as the basis for policymaking in our ratings-based communities. Given its rigorous nature, optimization provides not only an analytical tool by which to measure outcomes, but also a method by which political rancor can be reduced. Not many people will sustain emotional debate when faced with a requirement to produce objective functions. An objective function is simply an equation that tells us what variable we wan..." |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Main|System modeling}} |
{{Main|System modeling}} |
||
We have discussed optimization as the basis for policymaking in our ratings-based communities. Given its rigorous nature, optimization provides not only an analytical tool by which to measure outcomes, but also a method by which political rancor can be reduced. Not many people will sustain emotional [[debate]] when faced with a requirement to produce objective functions. |
We have discussed optimization as the basis for policymaking in our ratings-based communities. Given its rigorous nature, optimization provides not only an analytical tool by which to measure outcomes, but also a method by which political rancor can be reduced. For economic systems it provides the means to [[Democratizing resource allocation|democratize resource allocation]]. Not many people will sustain emotional [[debate]] when faced with a requirement to produce objective functions. |
||
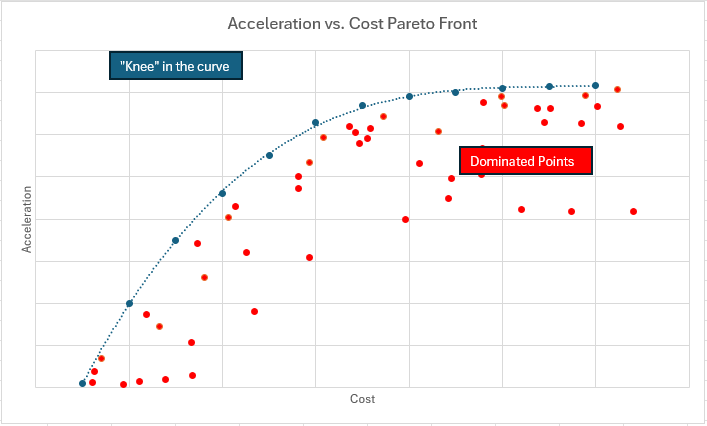
An objective function is simply an equation that tells us what variable we want to maximize or minimize as a function of its inputs. Let’s suppose we are designing a car and we want to minimize Cost and maximize Acceleration. Generally speaking, the more we are willing to pay for an engine, the more power we will get, and hence more acceleration. This will be true up to a point of diminishing returns where further power increases do very little to increase the acceleration. This has to do with the details of losses and power to weight ratios, which is beyond our scope here. Suffice it to say that at some point it will take a huge increase in cost to increase the acceleration only a little bit. We can express this tradeoff using the Pareto chart that we are all familiar with: |
An objective function is simply an equation that tells us what variable we want to maximize or minimize as a function of its inputs. Let’s suppose we are designing a car and we want to minimize Cost and maximize Acceleration. Generally speaking, the more we are willing to pay for an engine, the more power we will get, and hence more acceleration. This will be true up to a point of diminishing returns where further power increases do very little to increase the acceleration. This has to do with the details of losses and power to weight ratios, which is beyond our scope here. Suffice it to say that at some point it will take a huge increase in cost to increase the acceleration only a little bit. We can express this tradeoff using the Pareto chart that we are all familiar with: |
||
| Line 49: | Line 49: | ||
HDI also comes in a few adjusted forms, namely an inequality adjustment and a planetary-pressures adjustment (ie environmental impact). This has the result of changing the results a modest amount but it mainly reflects how a reliable baseline index can be modified to cope with new societal values. Our ratings based society will have the means to easily tinker with its objective function as it makes progress. |
HDI also comes in a few adjusted forms, namely an inequality adjustment and a planetary-pressures adjustment (ie environmental impact). This has the result of changing the results a modest amount but it mainly reflects how a reliable baseline index can be modified to cope with new societal values. Our ratings based society will have the means to easily tinker with its objective function as it makes progress. |
||
Other indexes of societal goodness include the [https://worldhappiness.report/ World Happiness Report] (WHR). It is based on a poll question which asks respondents to rate how satisfactory their lives are on a scale of 0 (worst possible life) to 10 (best possible life). It is then correlated with six measures: GDP per capita, social support, life expectancy, freedom to make your own choices, generosity of the general population, and perceptions of corruption. These six variables are used to explain the variations in the poll data across countries. This is a more subjective index than HDI and requires regular polling to achieve. However, a society based on regular ratings should have no trouble adjusting to this. As for creating an objective function, it is highly probable that an equation involving the six correlated variables could be developed. |
Other indexes of societal goodness include the [https://worldhappiness.report/ World Happiness Report] (WHR). It is based on a poll question which asks respondents to rate how satisfactory their lives are on a scale of 0 (worst possible life) to 10 (best possible life). It is then correlated with six measures: GDP per capita, social support, life expectancy, freedom to make your own choices, generosity of the general population, and perceptions of corruption. These six variables are used to explain the variations in the poll data across countries. This is a more subjective index than HDI and requires regular [[polling]] to achieve. However, a society based on regular ratings should have no trouble adjusting to this. As for creating an objective function, it is highly probable that an equation involving the six correlated variables could be developed. |
||
The WHR is significant because it was designed to contradict GDP per capita as the standard of societal wellness. It plays into several well-tested theories about income. One of these is the [https://en.wikipedia.org/wiki/Easterlin_paradox Easterlin Paradox] which posits that increased wealth increases individual happiness in the short term but does nothing in the long term. For various reasons, people have a way of returning to their baseline levels of happiness fairly quickly. Another is the observation that wealth increases happiness up to a certain level and then has only a small effect after that (https://www.pnas.org/doi/full/10.1073/pnas.1011492107). |
The WHR is significant because it was designed to contradict GDP per capita as the standard of societal wellness. It plays into several well-tested theories about income. One of these is the [https://en.wikipedia.org/wiki/Easterlin_paradox Easterlin Paradox] which posits that increased wealth increases individual happiness in the short term but does nothing in the long term. For various reasons, people have a way of returning to their baseline levels of happiness fairly quickly. Another is the observation that wealth increases happiness up to a certain level and then has only a small effect after that (https://www.pnas.org/doi/full/10.1073/pnas.1011492107). |
||
Revision as of 14:03, 13 September 2024
Main article: System modeling
We have discussed optimization as the basis for policymaking in our ratings-based communities. Given its rigorous nature, optimization provides not only an analytical tool by which to measure outcomes, but also a method by which political rancor can be reduced. For economic systems it provides the means to democratize resource allocation. Not many people will sustain emotional debate when faced with a requirement to produce objective functions.
An objective function is simply an equation that tells us what variable we want to maximize or minimize as a function of its inputs. Let’s suppose we are designing a car and we want to minimize Cost and maximize Acceleration. Generally speaking, the more we are willing to pay for an engine, the more power we will get, and hence more acceleration. This will be true up to a point of diminishing returns where further power increases do very little to increase the acceleration. This has to do with the details of losses and power to weight ratios, which is beyond our scope here. Suffice it to say that at some point it will take a huge increase in cost to increase the acceleration only a little bit. We can express this tradeoff using the Pareto chart that we are all familiar with:
This is an example of a multi-variable optimization problem. If we have exactly 2 objective variables, as above, then we will have a standard Pareto chart with each objective plotted against each other on an x-y graph. A 3-D version of this is possible with 3 variables but things get hard to see beyond this point, although there is no theoretical limit to how many objectives we can have.
It is certainly true that societies have multiple objectives. They are trying to improve housing, health, education, per capita income, etc. But it is probably better to use objectives that represent weighted aggregates of simpler objectives just so we can visualize our tradeoffs better.
One modern societal objective function is HDI, the human development index, created by the UNDP (United Nations Development Program). HDI represents a combination of life expectancy, educational level, and material standard of living (Income per capita). Each of these categories is itself an index.
The first is the Life Expectancy Index, LEI:
Note that LEI is 1 for life expectancy of 85 years and 0 for life expectancy of 20 years.
The second is the Education Index, EI:
where
– mean years of schooling for someone older than 25.
– expected years of schooling for someone under 18.
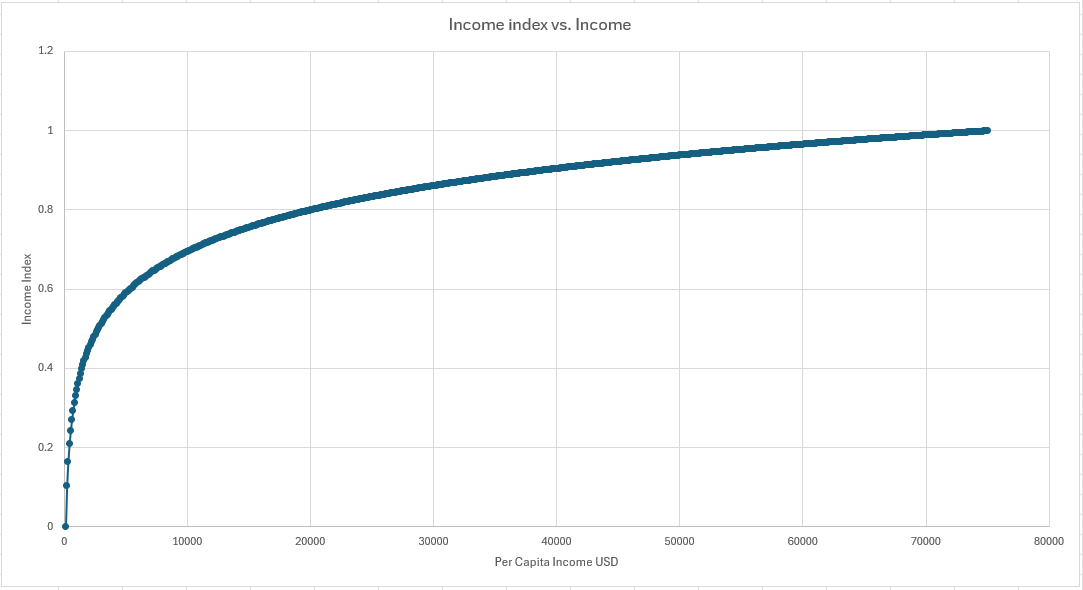
The third is the Income Index, II:
Putting these three together in a geometric mean results in the aggregate Human Development Index:
As we can see, the HDI is not difficult to compute and does not rely on sophisticated math. It is mainly a way to bring together 3 disparate measures by first creating a 0-1 scaled index for each of them and then taking their average. This essentially means we are weighting each sub-index equally.
The other essential task here is to decide what 0 and 1, the ends of the scale, mean. In the above, a life expectancy of 20 is 0 and 85 is 1. This is a community decision and is somewhat subjective. Alongside this, we need to decide on an appropriate function. All the functions expressed here are linear except for the Income Index, which is logarithmic:
The idea here is that, for lower incomes, small increases in income have a large impact of standard of living (which is what we’re ultimately trying to measure) but as income gets higher the increases stop having as much of an effect. Once folks have homes, adequate food, etc. income increases become less important. But before this point, they matter a lot.
This notion is also somewhat intuitive but we wouldn’t expect ordinary citizens to be able to express it mathematically. In these cases, a graphical tool that allows them to draw their intuitive feel for the function can be used and curve fitting software can be used to translate that to the required mathematical form. Software of this kind is widely available (eg https://grafiti.com/tablecurve2d/ , https://fityk.nieto.pl/ , etc.).
HDI also comes in a few adjusted forms, namely an inequality adjustment and a planetary-pressures adjustment (ie environmental impact). This has the result of changing the results a modest amount but it mainly reflects how a reliable baseline index can be modified to cope with new societal values. Our ratings based society will have the means to easily tinker with its objective function as it makes progress.
Other indexes of societal goodness include the World Happiness Report (WHR). It is based on a poll question which asks respondents to rate how satisfactory their lives are on a scale of 0 (worst possible life) to 10 (best possible life). It is then correlated with six measures: GDP per capita, social support, life expectancy, freedom to make your own choices, generosity of the general population, and perceptions of corruption. These six variables are used to explain the variations in the poll data across countries. This is a more subjective index than HDI and requires regular polling to achieve. However, a society based on regular ratings should have no trouble adjusting to this. As for creating an objective function, it is highly probable that an equation involving the six correlated variables could be developed.
The WHR is significant because it was designed to contradict GDP per capita as the standard of societal wellness. It plays into several well-tested theories about income. One of these is the Easterlin Paradox which posits that increased wealth increases individual happiness in the short term but does nothing in the long term. For various reasons, people have a way of returning to their baseline levels of happiness fairly quickly. Another is the observation that wealth increases happiness up to a certain level and then has only a small effect after that (https://www.pnas.org/doi/full/10.1073/pnas.1011492107).
Both of these indexes score advanced Western European democracies the highest (e.g. Finland, Switzerland) and war-ravaged already-poor countries the lowest (e.g. Afghanistan, South Sudan). This is obvious and, by and large, the trends in both these indexes are what anyone with a reasonable understanding of the world would expect. However, some countries manage to defy expectations. Costa Rica, for instance, ranks 12th in the Happiness Index but 64th in HDI. In other words, it ranks amongst the most advanced countries in the world in happiness but is only middling in terms of its own advancement. Or, perhaps, they know something we don’t. The US, btw, ranks 23rd in Happiness and 20th in HDI, not terrible but, considering its wealth, underwhelming.
It seems straightforward enough to just maximize HDI or Happiness. That would be a single variable optimization problem. But it’s probably more complicated given global warming. High HDI countries tend to be the highest carbon footprint countries. So we might choose to create a second objective related to environmental impact. A likely result is a Pareto chart in which HDI rises with environmental impact. We then choose how much our HDI is worth in terms of damage to the environment. This is why Costa Rica is intriguing. It has managed a relatively high HDI but is also one of the best performers on the environment. The US, incidentally, would not even be on the Pareto frontier given its lackluster HDI and poor environmental record.
It should be noted that both HDI and Happiness index are the result of dissatisfaction with GDP per capita as the sole measure of societal progress. GDP per capita has been, and still is to a large extent, the standard measure by which we rank societies. The US ranks 6th on this front, outranked by only vastly smaller countries, some of them insignificant (eg Monaco). Among world powers, the US has ranked 1st for about a century. The US is a prime example for why the GDP per capita is a poor measure of societal well-being. And its inability to change is further evidence that nation states, particularly big ones, are not ideal organizing principles for society.