More actions
No edit summary |
No edit summary |
||
| (36 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<h2>Some thoughts on evaluating |
<h2>Some thoughts on evaluating [[Argument|argument]]s</h2> |
||
Here we discuss how we might evaluate an argument made by a respondent instead of simply relying on the given [[Probability|probability]] (as we've been doing so far). An argument, assuming it is made public, could then be evaluated by the questioner and others independently to find a more accurate probability. This opens up a new idea in our work, that of assessing the truth by evaluating the reasoning put forth in an [[Opinion|opinion]]. |
|||
One idea for doing this starts with a simple model for argument construction. The argument consists of supporting |
One idea for doing this starts with a simple model for argument construction. The argument consists of [[Supporting statement|supporting statement]]s which are tied together with [[Logic|logic]] to form a conclusion. The conclusion is the answer to the overall question being asked of the network. Each supporting statement and the [[logic]] can be evaluated independently to determine the extent to which the conclusion is true. The following diagram illustrates this: |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 21: | Line 21: | ||
1 -> 4 [dir="back"]; |
1 -> 4 [dir="back"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
The probability of the supporting statements can be combined in a [[Bayes' theorem|Bayes]]ian manner. This is in keeping with the Bayesian idea of modifying prior probabilities given new evidence (ie supporting statements). These probabilities can be [[Trust|trust]]-modified as Sapienza proposed (https://ceur-ws.org/Vol-1664/w9.pdf) but since they are likely being assigned by the questioner, we will assume that [[trust]] is already built into them. Of more importance is the [[Relevance|relevance]] of the supporting statements. They can range from completely irrelevant to completely relevant. A completely relevant statement will take the full value of the probability it was originally assigned. A completely irrelevant statement would reduce the probability to 50%, where it will have no influence on the outcome. In that sense relevance functions in the same way trust does to modify the probability: |
|||
<math> |
|||
The probability of the supporting statements can be combined in a Bayesian manner. This is in keeping with the Bayesian idea of modifying prior probabilities given new evidence (ie supporting statements). These probabilities can be trust-modified as Sapienza proposed (https://ceur-ws.org/Vol-1664/w9.pdf) but since they are likely being assigned by the questioner, we will assume that trust is already built into them. Of more importance is the relevance of the supporting statements. They can range from completely irrelevant to completely relevant. A completely relevant statement will take the full value of the probability it was originally assigned. A completely irrelevant statement would reduce the probability to 50%, where it will have no influence on the outcome. In that sense relevance functions in the same way trust does to modify the probability: |
|||
$$ |
|||
P_{mod} = P_{nom} + R(P - P_{nom}) |
P_{mod} = P_{nom} + R(P - P_{nom}) |
||
</math> |
|||
$$ |
|||
where |
where |
||
<math>R</math> is relevance (0.0 - 1.0) |
|||
<math>P_{mod}</math> is relevance-modified probability |
|||
<math>P_{nom}</math> is the nominal probability (=0.5 for a [[Predicate|predicate]] question) |
|||
<math>P</math> is the unmodified probability |
|||
After the relevance-modification, each supporting statement is combined in the usual manner via Bayes. For the first two statements, |
After the relevance-modification, each supporting statement is combined in the usual manner via Bayes. For the first two statements, |
||
<math> |
|||
$$ |
|||
P_{comb1,2} = {P_{s1}P_{s2}\over {P_{s1}P_{s2} + (1-P_{s1})(1-P_{s2})}} |
P_{comb1,2} = {P_{s1}P_{s2}\over {P_{s1}P_{s2} + (1-P_{s1})(1-P_{s2})}} |
||
</math> |
|||
$$ |
|||
and so on for each additional statement. Here it is to be understood that |
and so on for each additional statement. Here it is to be understood that <math>P_{s1}</math>, etc. is the value <i>after</i> the relevance modification. |
||
Logic will also have a probability assigned to it to represent its quality. A fully illogical argument would receive a 0, which when combined via Bayes with the supporting statements would render the probability of the entire argument 0. This makes sense because a completely illogical argument, regardless of the strength of its supporting statements, destroys itself. A fully logical argument, however, will not receive a 1 but rather a 0.5. When combined with the supporting statements a 1 would render the final probability a 1, which is not reasonable. A 0.5, however, would do nothing and the final probability would be the combined probability of the supporting statements. Thus we assume that perfect logic is neutral and less than perfect logic reduces the combined probability of the statements. Again, this seems reasonable. We expect, by default, logical arguments which then rest on the strength of their supporting statements. If we notice flaws in the logic we discount the strength of the argument accordingly. |
Logic will also have a probability assigned to it to represent its quality. A fully illogical argument would receive a 0, which when combined via Bayes with the supporting statements would render the probability of the entire argument 0. This makes sense because a completely illogical argument, regardless of the strength of its supporting statements, destroys itself. A fully logical argument, however, will not receive a 1 but rather a 0.5. When combined with the supporting statements a 1 would render the final probability a 1, which is not reasonable. A 0.5, however, would do nothing and the final probability would be the combined probability of the supporting statements. Thus we assume that perfect logic is neutral and less than perfect logic reduces the combined probability of the statements. Again, this seems reasonable. We expect, by default, logical arguments which then rest on the strength of their supporting statements. If we notice flaws in the logic we discount the strength of the argument accordingly. |
||
| Line 52: | Line 51: | ||
Let's try an example with these ideas: |
Let's try an example with these ideas: |
||
Question: |
Question: Are humans causing frog populations to decline?<br> |
||
Answer / Conclusion: Man made climate change is real.<br> |
|||
Answer / Conclusion: Yes, mankind is causing a fall in frog populations.<br> |
|||
Logic: Mankind is causing climate change if we can show that the earth's temperature is changing over time and can show a human behavior that makes the temperature change.<br> |
|||
Logic: Mankind is causing the fall of frog populations if we can show that frog populations are decreasing over time and can show a human behavior that causes the decline.<br> |
|||
Supporting Statements:<br> |
Supporting Statements:<br> |
||
1. The average earth temperature has gone up by 2 deg F since the late 19th century (https://climate.nasa.gov/evidence/#footnote_4) |
|||
2. My wife complained about the heat this summer. |
|||
3. Scientists say the oceans are getting warmer, ice caps are melting, and glaciers are retreating. |
|||
# [https://en.wikipedia.org/wiki/Frog#:~:text=Frog%20populations%20have%20declined%20significantly%20since%20the%201950s. Frog populations have declined since the 1950's.] |
|||
We start by judging the quality of the supporting statements. 1 seems like a well substantiated statement (a high P) but is not completely relevant because it only hints at human involvement. 2 is completely true but irrelevant. 3 is a contributor but seems less substantiated than 1 and contains no human cause. We proceed by assigning probability and relevance values: |
|||
# My wife complained that she doesn't see frogs anymore. |
|||
# [https://wwf.panda.org/discover/our_focus/freshwater_practice/freshwater_biodiversity_222/ Scientists say] that the loss of freshwater habitats has affected frog populations. |
|||
We start by judging the quality of the supporting statements. 1 seems like a well substantiated statement (a high P) but is not completely relevant because it only hints at human involvement. 2 is completely true but mostly irrelevant. 3 is a contributor but seems less substantiated than 1 and contains no human cause. We proceed by assigning probability and relevance values: |
|||
<math>P_{s1}=0.9</math> |
|||
<math>R_{s1}=0.7</math> |
|||
<math>P_{s1mod} = 0.5 + 0.7(0.9 - 0.5) = 0.78</math> |
|||
<math>P_{s2}=1.0</math> |
|||
<math>R_{s2}=0.0</math> |
|||
<math>P_{s2mod} = 0.5 + 0.0(1.0 - 0.5) = 0.5</math> |
|||
<math>P_{s3}=0.75</math> |
|||
<math>R_{s3}=0.5</math> |
|||
<math>P_{s3mod} = 0.5 + 0.5(0.75 - 0.5) = 0.625</math> |
|||
Since s2 won't count in the Bayesian calculation we can ignore it and: |
Since s2 won't count in the Bayesian calculation we can ignore it and: |
||
<math>P_{comb,s} = {(0.78)(0.625) \over {0.78(0.625)+0.22(0.375)}} = 0.855</math> |
|||
The logic/conclusion in this case is reasonably strong so we will assign it a high value, say |
The logic/conclusion in this case is reasonably strong so we will assign it a high value, say <math>P_l = 0.45</math> (remember, out of 0.5). It could be improved by observing that the word "behavior" is too general and should be replaced by, say, "policy choice" (ie urban growth into ecologically important wetlands). We note here that logic is more than just the mathematical construction of an argument. Since we are speaking a human language, logic might also be flawed because it uses imprecise wording. |
||
Putting |
Putting <math>P_{comb,s}</math> together with <math>P_l</math> using Bayes we obtain a concluding probability: |
||
<math>P_c = {0.855(0.45) \over {{0.855(0.45) + 0.145(0.55)}}} = 0.82</math> |
|||
One potential pitfall of this model is that repetitive supporting statements of high probability will quickly render a combined probability near 1.0. As we've seen in the past, this is simply the result of the Bayes equation. The user would need to watch for attempts like these to distort the answer by removing repetitive statements or making them irrelevant. |
One potential pitfall of this model is that repetitive supporting statements of high probability will quickly render a combined probability near 1.0. As we've seen in the past, this is simply the result of the Bayes equation. The user would need to watch for attempts like these to distort the answer by removing repetitive statements or making them irrelevant. |
||
| Line 90: | Line 93: | ||
<h2>Scoring of individual arguments</h2> |
<h2>Scoring of individual arguments</h2> |
||
Arguments can be scored on [[Veracity|veracity]], impact, relevance, clarity, and informal quality (lack of fallacies): |
|||
[Last time](More argument mapping tools and proposed ideas for our own such tool) we discussed some criteria for argument scoring: |
|||
- Veracity is how true the argument is based on source information. Source information itself will be scored: <math>V</math> |
|||
- Veracity, $V$ |
|||
- Impact & Relevance, $R$ |
|||
- Clarity, $C$ |
|||
- Informal Quality (extent to which argument is free of fallacies), $F$ |
|||
- Impact & Relevance is how deeply the argument affects the main contention of the [[debate]] (or the argument immediately above): <math>R</math> |
|||
- Clarity is how understandable the argument is: <math>C</math> |
|||
- Informal quality (lack of fallacies) is whether the argument commits any logical fallacies of its own. A list of informal fallacies (and formal ones) will be provided to help users select appropriately: <math>F</math> |
|||
Since Impact and Relevance are closely related concepts we will merge these into one, Relevance. The simplest method for combining these is to average them, or weighted average them: |
Since Impact and Relevance are closely related concepts we will merge these into one, Relevance. The simplest method for combining these is to average them, or weighted average them: |
||
<math> |
|||
$$ |
|||
S = w_vV + w_rR + w_cC + w_fF |
S = w_vV + w_rR + w_cC + w_fF |
||
</math> |
|||
$$ |
|||
where |
where |
||
<math>w_x</math> is a weighting for category X (eg Veracity, Relevance, etc) |
|||
<math>w_v + w_r + w_c + w_f = 1</math> |
|||
This seems reasonable and if we believe that certain criteria should weigh more (such as Veracity) we can easily make the weighting factors reflect this. However, intuitively it seems that a category such as Veracity should not only weigh more but have the power to take down the whole argument. After all, if the argument is a straightforward lie, it should receive a score of zero, regardless of its other attributes (such as relevance, clarity, etc): |
This seems reasonable and if we believe that certain criteria should weigh more (such as Veracity) we can easily make the weighting factors reflect this. However, intuitively it seems that a category such as Veracity should not only weigh more but have the power to take down the whole argument. After all, if the argument is a straightforward lie, it should receive a score of zero, regardless of its other attributes (such as relevance, clarity, etc): |
||
<i>Who is the best choice for President? |
<i>Who is the best choice for President? X is the best choice because he will land a person on Mars in his first year.</i> |
||
This argument is a lie and although it is clear, has no evident fallacies, and is relevant to the question at hand, it should be thrown out. |
This argument is a lie and although it is clear, has no evident fallacies, and is relevant to the question at hand, it should be thrown out. |
||
| Line 118: | Line 123: | ||
The same can be said of Relevance. A completely irrelevant argument should also have the power to render the whole argument moot: |
The same can be said of Relevance. A completely irrelevant argument should also have the power to render the whole argument moot: |
||
<i>Who is the best choice for President? |
<i>Who is the best choice for President? X is the best choice because he likes pizza and so do I.</i> |
||
With this in mind, we can propose the following equation, which we will dub the "VRFC equation": |
With this in mind, we can propose the following equation, which we will dub the "VRFC equation": |
||
<math> |
|||
$$ |
|||
S = VR(w_fF + w_cC) |
S = VR(w_fF + w_cC) |
||
</math> |
|||
$$ |
|||
Where |
Where |
||
<math>S</math> = Score for the argument which varies from 0-1 |
|||
<math>w_f</math> = weighting factor for Fallacies. |
|||
<math>w_c</math> = weighting factor for Clarity. |
|||
<math>w_f + w_c = 1</math> |
|||
and each of the constituent variables ( |
and each of the constituent variables (<math>V, R, F, C</math>) has a range 0-1. |
||
In this equation either Veracity or Relevance have the power to nullify the entire argument. Similarly a combination of Fallacies and lack of Clarity can do the same. However, a fallacious argument alone seems like it could still have merit, as would an argument whose only flaw was lack of clarity: |
In this equation either Veracity or Relevance have the power to nullify the entire argument. Similarly a combination of Fallacies and lack of Clarity can do the same. However, a fallacious argument alone seems like it could still have merit, as would an argument whose only flaw was lack of clarity: |
||
<i>We should support |
<i>We should support Czechoslovakia because if the Nazi's prevail they will conquer the world.</i> |
||
This argument commits the slippery slope fallacy but is not entirely invalid. Similarly an unclear argument can still manage to make a point: |
This argument commits the slippery slope [[Fallacy|fallacy]] but is not entirely invalid. Similarly an unclear argument can still manage to make a point: |
||
<i>We should support |
<i>We should support Europe because first the Sudetenland, then the Czechs, and soon enough it's over when all the Brits had to do was get rid of that weakling sooner.</i> |
||
It would seem that a fallacious argument should weigh more than an unclear one. Proposed weights might be: |
It would seem that a fallacious argument should weigh more than an unclear one. Proposed weights might be: |
||
<math>w_f = 0.7, w_c = 0.3</math> |
|||
<h3>Rolling up the score of argument trees</h3> |
<h3>Rolling up the score of argument trees</h3> |
||
| Line 157: | Line 163: | ||
Here we develop a proposed equation for rolling up the score for an argument based on its own score and that of its sub-arguments. In doing so we emphasize that any argument can stand on its own and be scored in the absence of sub-arguments. This creates an interesting dynamic. The sub-argument may bolster or detract from the parent argument but the extent to which it does should be limited. |
Here we develop a proposed equation for rolling up the score for an argument based on its own score and that of its sub-arguments. In doing so we emphasize that any argument can stand on its own and be scored in the absence of sub-arguments. This creates an interesting dynamic. The sub-argument may bolster or detract from the parent argument but the extent to which it does should be limited. |
||
Furthermore, once the sub-argument becomes weaker than a certain threshold, it should stop influencing the parent argument altogether. Here, we will set this threshold at 0.5. Thus only Pro sub-arguments that score 0.5 or better will have any influence on the parent argument. For Con sub-arguments we will use the same threshold but first modify the sub-argument score by |
Furthermore, once the sub-argument becomes weaker than a certain threshold, it should stop influencing the parent argument altogether. Here, we will set this threshold at 0.5. Thus only Pro sub-arguments that score 0.5 or better will have any influence on the parent argument. For Con sub-arguments we will use the same threshold but first modify the sub-argument score by <math>1-S</math>. Thus a strong Con sub-argument, scoring say 0.9, would enter the calculation with a score of 0.1. The result is a range of scores 0-1 of which 0-0.5 is Con and 0.5-1 is Pro. Scores of exactly 0.5 are neutral. |
||
Let's consider the case with one argument and one pro sub-argument and one Con sub-argument. |
Let's consider the case with one argument and one pro sub-argument and one Con sub-argument. |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 173: | Line 179: | ||
0 -> 2 [dir="both"]; |
0 -> 2 [dir="both"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
In this case the argument's score is 0.9, and both the Pro/Con sub-argument score is 0.7. These numbers would normally be arrived at by using the VRFC eqn above, but we will just assume them for now. The first sub-argument, in this case, bolsters the argument because it is a Pro argument and has a score (0.7) greater than 0.5. The second sub-argument, with the same score, detracts from the argument because it is on the Con side. We emphasize that if these scores were at or below 0.5 they would have no effect on the argument. |
In this case the argument's score is 0.9, and both the Pro/Con sub-argument score is 0.7. These numbers would normally be arrived at by using the VRFC eqn above, but we will just assume them for now. The first sub-argument, in this case, bolsters the argument because it is a Pro argument and has a score (0.7) greater than 0.5. The second sub-argument, with the same score, detracts from the argument because it is on the Con side. We emphasize that if these scores were at or below 0.5 they would have no effect on the argument. |
||
| Line 180: | Line 186: | ||
For |
For <math>s > 0.5</math> and <math>x > 0.5</math> |
||
<math> |
|||
$$ |
|||
s_{mod} = 2(1-s)fx + s - (1-s)f |
s_{mod} = 2(1-s)fx + s - (1-s)f |
||
</math> |
|||
$$ |
|||
For |
For <math>s > 0.5</math> and <math>x <= 0.5</math> |
||
<math> |
|||
$$ |
|||
s_{mod} = s |
s_{mod} = s |
||
</math> |
|||
For |
For <math>s < 0.5</math> and </math>x > 0.5</math> |
||
<math> |
|||
$$ |
|||
s_{mod} = 2sfx + s - sf |
s_{mod} = 2sfx + s - sf |
||
</math> |
|||
$$ |
|||
For |
For <math>s < 0.5</math> and <math>x <= 0.5</math> |
||
<math> |
|||
$$ |
|||
s_{mod} = s |
s_{mod} = s |
||
</math> |
|||
$$ |
|||
where |
where |
||
<math>s</math> = score for parent argument |
|||
<math>x = x_p</math> = score for Pro arguments |
|||
<math>x = 1-x_c</math> = score for Con arguments |
|||
<math>f</math> = maximum possible fraction of increase possible, 0-1 |
|||
The variable |
The variable <math>f</math> is a user selected number between 0-1 and represents the extent to which the sub-argument score can be affected. For example, a sub-argument with x = 0.9, as in the diagram above, can be improved by 0.1 to a maximum of 1. Then <math>f</math> represents the fraction of 0.1 that we will allow for our improvement. If <math>f = 0.25</math>, for instance, then the maximum range around 0.9 that the sub-argument can affect is <math>(0.25)(0.1) = 0.025</math>. Thus the maximum score the argument can have is 0.925 and the minimum is 0.875. |
||
For the argument above: |
For the argument above: |
||
<math>s = 0.9</math> |
|||
<math>f = 0.25</math> User input |
|||
For the Pro sub-argument: |
For the Pro sub-argument: |
||
<math>x = x_p = 0.7</math> |
|||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.9)(0.25)(0.7) + 0.9 - (1-0.9)(0.25) = 0.91</math> |
|||
For the Con sub-argument: |
For the Con sub-argument: |
||
<math>x = (1-x_c) = (1-0.7) = 0.3</math> |
|||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.9)(0.25)(0.3) + 0.9 - (1-0.9)(0.25) = 0.89</math> |
|||
We can see here that the Pro and Con sub-arguments exactly balance each other since they both have the same score. |
We can see here that the Pro and Con sub-arguments exactly balance each other since they both have the same score. |
||
| Line 240: | Line 246: | ||
 |
 |
||
One important property of this equation is that the stronger (or weaker) an argument becomes, it becomes harder for a sub-argument to change it. This is because the maximum allowed movement is |
One important property of this equation is that the stronger (or weaker) an argument becomes, it becomes harder for a sub-argument to change it. This is because the maximum allowed movement is <math>1-s</math> if <math>s > 0.5</math> or simply <math>s</math> if <math>s <= 0.5</math>. The idea behind this property is that very strong arguments should be harder to dislodge precisely because they have covered themselves well. A weaker argument, for instance one that fails to mention an obvious supporting fact, is in a position to be bolstered more by a sub-argument which mentions the fact. Similarly a very weak argument should be difficult to bolster. If the argument is a lie or irrelevant, for instance, there isn't much that can be done to rescue it. |
||
This property has the further consequence that |
This property has the further consequence that <math>s</math> cannot be changed by the sub-arguments if it is 1 or 0. A truly perfect argument, <math>s = 1</math>, cannot be weakened no matter how strong its Con sub-argument. Similarly a perfectly flawed argument, <math>s = 0</math> cannot be bolstered with any Pro sub-argument. We will discuss below a method to deal with the fact that, regardless of the quality of the argument, users may still vote to score arguments 1 or 0. |
||
<h4>Population adjustments</h4> |
<h4>Population adjustments</h4> |
||
| Line 250: | Line 256: | ||
Here we propose a simple modification factor, based on the ratio of users voting for each argument/sub-argument: |
Here we propose a simple modification factor, based on the ratio of users voting for each argument/sub-argument: |
||
<math>s_{mod,pop} = (s_{mod} - s){p_s\over p} + s</math> |
|||
where |
where |
||
<math>s_{mod,pop}</math> is the population modified score |
|||
<math>s_{mod}</math> is the modified score without population modifications (see above) |
|||
<math>p_s</math> is the population voting for the sub-argument |
|||
<math>p</math> is the population voting for the parent argument |
|||
<math>s</math> is the original score of the parent argument |
|||
Usually we expect that sub-arguments will receive fewer votes than parent arguments, so |
Usually we expect that sub-arguments will receive fewer votes than parent arguments, so <math>{{p_s\over p} <= 1}</math> in general. For the case when <math>p_s > p</math> we will force <math>{p_s\over p} = 1</math>. Therefore there is no danger that a sub-argument can overwhelm a parent argument by voting power alone. This is in keeping with our philosophy that sub-arguments can have at best a limited effect on parent arguments. |
||
<h4>Example calculation</h4> |
<h4>Example calculation</h4> |
||
Let's do a problem with the following argument tree and |
Let's do a problem with the following argument tree and <math>f=0.25</math>: |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 294: | Line 300: | ||
0 -> 8 [dir="both"]; |
0 -> 8 [dir="both"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
Our objective here is to roll up the score for the Pro side of this tree. The Con side would be calculated similarly and we will skip this for the sake of brevity. Note that |
Our objective here is to roll up the score for the Pro side of this tree. The Con side would be calculated similarly and we will skip this for the sake of brevity. Note that <math>s</math> stands for the score and <math>p</math> is the population voting to produce that score. We start at the bottom, with the 2-3-4 portion of the tree, and for the sake of consistency with the above calculation we will recast <math>x_p</math> for 2 as <math>s</math> and label the population of the sub-arguments as <math>p_s</math>. |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 310: | Line 316: | ||
2 -> 4 [dir="both"]; |
2 -> 4 [dir="both"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
For the Pro sub-argument, we write: |
For the Pro sub-argument, we write: |
||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.7)(0.25)(0.8) + 0.7 - (1-0.7)(0.25) = 0.745</math> |
|||
We modify this by the respective populations: |
We modify this by the respective populations: |
||
<math>s_{mod,pop23} = (s_{mod} - s){p_s\over p} + s = (0.745 - 0.7){26\over 55} + 0.7 = 0.721</math> |
|||
For the Con sub-argument we first modify its score, |
For the Con sub-argument we first modify its score, |
||
<math>x = 1 - x_c = 0.4</math> |
|||
and write |
and write |
||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.7)(0.25)(0.4) + 0.7 - (1-0.7)(0.25) = 0.685</math> |
|||
and modify by the respective population, |
and modify by the respective population, |
||
<math>s_{mod,pop24} = (s_{mod} - s){p_s\over p} + s = (0.685 - 0.7){30\over 55} + 0.7 = 0.692</math> |
|||
These two values of |
These two values of <math>s_{mod,pop}</math> can now be combined to create a new <math>s</math> for the Pro argument: |
||
<math>s_{mod,tot} = (s_{mod,pop23} - s) + (s_{mod,pop24} - s) + s = (0.721 - 0.7) + (0.692 - 0.7) + 0.7 = 0.713</math> |
|||
We note here that the Pro argument got a little stronger as a result of its sub-arguments. The Pro sub-argument was substantially stronger than the Con sub-argument and, although fewer people voted for it, the population difference was not large. |
We note here that the Pro argument got a little stronger as a result of its sub-arguments. The Pro sub-argument was substantially stronger than the Con sub-argument and, although fewer people voted for it, the population difference was not large. |
||
| Line 340: | Line 346: | ||
For the Con sub-argument 5-6-7 we have the following situation: |
For the Con sub-argument 5-6-7 we have the following situation: |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 352: | Line 358: | ||
5 -> 7 [dir="both"]; |
5 -> 7 [dir="both"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
Here, for the Pro sub-argument, we first modify its score since it is the opposite of its parent. It is as if the parent were a Pro argument and the child were a Con argument. |
Here, for the Pro sub-argument, we first modify its score since it is the opposite of its parent. It is as if the parent were a Pro argument and the child were a Con argument. |
||
<math>x = 1 - x_p = 1 - 0.85 = 0.15</math> |
|||
We then proceed as usual with the calculation: |
We then proceed as usual with the calculation: |
||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.7)(0.25)(0.15) + 0.7 - (1-0.7)(0.25) = 0.6475</math> |
|||
<math>s_{mod,pop56} = (s_{mod} - s){p_s\over p} + s = (0.6475 - 0.7){19\over 43} + 0.7 = 0.677</math> |
|||
For the Con sub-argument |
For the Con sub-argument <math>x = x_c = 0.95</math> since the parent argument is also Con: |
||
<math>s_{mod} = 2(1-s)fx + s - (1-s)f = 2(1-0.7)(0.25)(0.95) + 0.7 - (1-0.7)(0.25) = 0.7675</math> |
|||
<math>s_{mod,pop57} = (s_{mod} - s){p_s\over p} + s = (0.7675 - 0.7){28\over 43} + 0.7 = 0.744</math> |
|||
We combine these two results in the same manner as above: |
We combine these two results in the same manner as above: |
||
<math>s_{mod,tot} = (s_{mod,pop56} - s) + (s_{mod,pop57} - s) + s = (0.677 - 0.7) + (0.744 - 0.7) + 0.7 = 0.721</math> |
|||
With the bottom layer of the tree calculated, we have the following situation: |
With the bottom layer of the tree calculated, we have the following situation: |
||
<kroki lang="graphviz"> |
|||
digraph G { |
digraph G { |
||
fontname="Helvetica,Arial,sans-serif" |
fontname="Helvetica,Arial,sans-serif" |
||
| Line 392: | Line 398: | ||
0 -> 8 [dir="both"]; |
0 -> 8 [dir="both"]; |
||
} |
} |
||
</kroki> |
|||
``` |
|||
All that remains is to calculate the 1-2-5 portion, which is very similar to the 2-3-4 calculation performed above. Therefore will skip the details of this and simply report the results: |
All that remains is to calculate the 1-2-5 portion, which is very similar to the 2-3-4 calculation performed above. Therefore will skip the details of this and simply report the results: |
||
<math>s_{mod,pop12} = 0.906</math> |
|||
<math>s_{mod,pop15} = 0.895</math> |
|||
<math>s_{mod, tot} = 0.901</math> |
|||
We see here that the final result is not much different than the original |
We see here that the final result is not much different than the original <math>s = 0.9</math>. This is a result of the Pro sub-arguments essentially being cancelled by the Con sub-arguments. Such a result is to be expected in many cases. |
||
In this example, we are skipping the Con side of the overall argument (node 8 in the tree above) because it would be exactly the same as what we have shown. If it had been calculated we would then combine the result for 1 and 8 to produce an overall score for the argument. |
In this example, we are skipping the Con side of the overall argument (node 8 in the tree above) because it would be exactly the same as what we have shown. If it had been calculated we would then combine the result for 1 and 8 to produce an overall score for the argument. |
||
The calculations above can be performed with the [attached snippet](https://gitlab.syncad.com/ |
The calculations above can be performed with the [attached snippet](https://gitlab.syncad.com/[[Peer|peer]]verity/trust-model-playground/-/snippets/164). The user input portion of the snippet is set up for the calculation we did immediately above: |
||
<syntaxhighlight lang="python"> |
|||
```python |
|||
#User input |
#User input |
||
side_parent = 'pro' #side, pro or con, that the parent argument is on |
side_parent = 'pro' #side, pro or con, that the parent argument is on |
||
| Line 419: | Line 425: | ||
ps_con_arr = [43.0] #pop voting for each con child sub-argument |
ps_con_arr = [43.0] #pop voting for each con child sub-argument |
||
mods_if1or0 = True #True if we want scores of 1 or 0 to be modified to near 1 or 0 (otherwise they can't be adjusted by this calculation) |
mods_if1or0 = True #True if we want scores of 1 or 0 to be modified to near 1 or 0 (otherwise they can't be adjusted by this calculation) |
||
</syntaxhighlight> |
|||
``` |
|||
To note, the snippet contains arrays to handle any number of child arguments. These are combined in the same way we combined the single Pro and Con argument above. |
To note, the snippet contains arrays to handle any number of child arguments. These are combined in the same way we combined the single Pro and Con argument above. |
||
Another variable, `mods_if1or0` controls whether we allow |
Another variable, `mods_if1or0` controls whether we allow <math>s</math> to be modified when it is set to 1 or 0. As discussed above, arguments where <math>s = 1</math> or <math>s = 0</math> are perfect, or perfectly flawed, and thus cannot be changed with sub-arguments. This idea may be theoretically plausible but it wouldn't stop users from voting 1 or 0 for arguments. In such cases the `mods_if1or0` switch, when True, changes <math>s</math> to 0.99 and 0.01 respectively. |
||
As a side note, this property is similar to Bayesian probabilities of 1 or 0 which also cannot be changed. We have discussed this problem in earlier posts under the guise that 1 or 0 probabilities don't really exist because they would require an infinite sample size. In the same way, a perfect argument (or perfectly imperfect) argument cannot exist because it would, at some point, run into the same issues that Bayesian probabilities do. |
As a side note, this property is similar to Bayesian probabilities of 1 or 0 which also cannot be changed. We have discussed this problem in earlier posts under the guise that 1 or 0 probabilities don't really exist because they would require an infinite sample size. In the same way, a perfect argument (or perfectly imperfect) argument cannot exist because it would, at some point, run into the same issues that Bayesian probabilities do. |
||
| Line 429: | Line 435: | ||
For example, suppose we've invented a pill that cures cancer. It is one dose, costs 10 cents to make, has no side effects, has no environmental impact due to manufacture, and is certain to cure someone's cancer. The argument for a cancer patient taking the pill is, for all practical purposes, perfect. There is simply no plausible argument against it. We could score such an argument a 1 until we remember our probabilities. We only know the pill works and has no side effects on a limited population, say 100,000 patients. We don't know what effect it will have on the 100,001st patient. So the best we can say is that the drug is 0.99999 effective. Given that the argument is really predicated on the effectiveness of the drug we could say its score is also 0.99999. |
For example, suppose we've invented a pill that cures cancer. It is one dose, costs 10 cents to make, has no side effects, has no environmental impact due to manufacture, and is certain to cure someone's cancer. The argument for a cancer patient taking the pill is, for all practical purposes, perfect. There is simply no plausible argument against it. We could score such an argument a 1 until we remember our probabilities. We only know the pill works and has no side effects on a limited population, say 100,000 patients. We don't know what effect it will have on the 100,001st patient. So the best we can say is that the drug is 0.99999 effective. Given that the argument is really predicated on the effectiveness of the drug we could say its score is also 0.99999. |
||
<h3>[ |
<h3>[https://slashdot.org/ Slashdot]</h3> |
||
Slashdot offers a system for content moderation summarized by the following from [wikipedia:Slashot|wikipedia]: |
|||
::<i>Slashdot's editors are primarily responsible for selecting and editing the primary stories that are posted daily by submitters. The editors provide a one-paragraph summary for each story and a link to an external website where the story originated. Each story becomes the topic for a threaded discussion among the site's users. A user-based moderation system is employed to filter out abusive or offensive comments.[63] Every comment is initially given a score of −1 to +2, with a default score of +1 for registered users, 0 for anonymous users (Anonymous Coward), +2 for users with high "karma", or −1 for users with low "karma". As [[Moderator|moderator]]s read comments attached to articles, they click to moderate the comment, either up (+1) or down (−1). Moderators may choose to attach a particular descriptor to the comments as well, such as "normal", "offtopic", "flamebait", "troll", "redundant", "insightful", "interesting", "informative", "funny", "overrated", or "underrated", with each corresponding to a −1 or +1 rating. So a comment may be seen to have a rating of "+1 insightful" or "−1 troll".[57] Comments are very rarely deleted, even if they contain hateful remarks. |
|||
::Starting in August 2019 anonymous comments and postings have been disabled. |
|||
::Moderation points add to a user's rating, which is known as "karma" on Slashdot. Users with high "karma" are eligible to become moderators themselves. The system does not promote regular users as "moderators" and instead assigns five moderation points at a time to users based on the number of comments they have entered in the system – once a user's moderation points are used up, they can no longer moderate articles (though they can be assigned more moderation points at a later date). Paid staff editors have an unlimited number of moderation points. A given comment can have any integer score from −1 to +5, and registered users of Slashdot can set a personal threshold so that no comments with a lesser score are displayed. For instance, a user reading Slashdot at level +5 will only see the highest rated comments, while a user reading at level −1 will see a more "unfiltered, anarchic version". A meta-moderation system was implemented on September 7, 1999,to moderate the moderators and help contain abuses in the moderation system. Meta-moderators are presented with a set of moderations that they may rate as either fair or unfair. For each moderation, the meta-moderator sees the original comment and the reason assigned by the moderator (e.g. troll, funny), and the meta-moderator can click to see the context of comments surrounding the one that was moderated.</i> |
|||
Slashdot's purpose is to promote high quality discussion which is somewhat similar to our purpose of promoting high quality arguments. In particular, the [[Reputation|reputation]] (karma) of the moderators is an interesting concept. We could use a similar system to weight voters with a good reputation higher in their argument scoring. Another interesting idea is the use of word descriptors to match scores. In our system descriptors such as "Completely irrelevant", "somewhat irrelevant", etc. could be a useful way to break up corresponding numerical ranges in our 0-1 scoring system. |
|||
<h2>Refining our Argument Score with Reputation/Trust</h2> |
|||
[[#Scoring of individual arguments|Above]] we discussed an equation to score arguments on the basis of Veracity, Relevance, Freedom from Fallacies, and Clarity: |
|||
<math> |
|||
S = VR(w_fF + w_cC) |
|||
</math> |
|||
Where |
|||
<math>S</math> is overall score |
|||
<math>V</math> is Veracity |
|||
<math>R</math> is Relevance |
|||
<math>F</math> is Fallacies (ie freedom from fallacies) |
|||
<math>C</math> is Clarity |
|||
<math>w_f</math> is weighting for Fallacies, eg 0.7 |
|||
<math>w_c</math> is weighting for Clarity, eg 0.3 |
|||
<math>w_f + w_c = 1</math> |
|||
Each user would vote on each category and the resulting <math>S</math> would be calculated. However, each user may have a different reputation/trust for their ability to judge these four criteria. We can take this into account by simply adding a weighting factor for Trust: |
|||
<math> |
|||
S = (T_vV)(T_rR)(w_fT_fF + w_cT_cC) |
|||
</math> |
|||
where |
|||
<math>T_x</math> = Trust in user's ability to evaluate each category <math>x</math> (Veracity, Relevance, Fallacies, and Clarity) |
|||
Since the user evaluates trust in multiple categories, it would be useful to generate a composite trust for all the categories: |
|||
<math> |
|||
T_{comp} = {(T_vV)(T_rR)(w_fT_fF + w_cT_cC) \over{VR(w_fF + w_cC)}} |
|||
</math> |
|||
Where |
|||
<math>T_{comp}</math> is the composite trust for all categories. |
|||
Note that <math>T_{comp}</math> can also be seen as an "average" trust, ie the single factor that produces the same argument score as that resulting from the multiple trust factors. |
|||
Once we have <math>T_{comp}</math> we can use it to generate an average <math>S</math> for all users: |
|||
<math> |
|||
S_{ave} = {\sum S \over{\sum T_{comp}}} |
|||
</math> |
|||
That is, instead of dividing by the number of people voting, we divide by the total of how much they "count". This is similar to the [trust-weighted average scheme]([[A trust weighted averaging technique to supplement straight averaging and Bayes]]) we have proposed before. It is this average <math>S</math> that we will take to be the score for the argument. |
|||
<h3>Rhetorical vs. [[Practical argument|Practical Argument]]s</h3> |
|||
So far our scoring methodology has been focused mainly on rhetorical aspects of arguments. Is the argument true, relevant to its parent contention, clear, and logical? These criteria certainly touch on the practical impact an argument may have and so far we have been merging Impact with Relevance since it is hard to distinguish the two. Consider the following: |
|||
<kroki lang="graphviz"> |
|||
digraph G { |
|||
fontname="Helvetica,Arial,sans-serif" |
|||
node [fontname="Helvetica,Arial,sans-serif"] |
|||
edge [fontname="Helvetica,Arial,sans-serif"] |
|||
layout=dot |
|||
0 [label="0, Argument: Biden is a good President because he got an infrastructure \n bill passed that will do good things for the whole country."] |
|||
1 [label="1, Sub-argument: The bill provides $2.9 million \n to Roanoke airport for improvements."] |
|||
2 [label = "2, Sub-argument: The bill provides $150 billion \n to combat climate change."] |
|||
0 -> 1 [dir="forward"]; |
|||
0 -> 2 [dir="forward"]; |
|||
} |
|||
</kroki> |
|||
Here it would seem appropriate to roll Impact into Relevance. Presumably most voters will recognize Sub-argument 2 as being the more relevant one simply because it is, on a practical level, the more impactful one. |
|||
However, usually Relevance is a rhetorical quality, not a practical one. In this case, as a matter of rhetoric, both supporting arguments are relevant to the topic at hand. They are both, without question, part of Biden's infrastructure bill. They are both true, clear, and free of fallacies. But even so, although it is clear what is going on, it would be better to separate the issue of whether Biden is a good president from the issue of which infrastructure allocations add the most value. |
|||
One reason for this separation, in terms of the [math laid out previously](Argument scoring), is that a weak sub-argument stops having any influence once its score goes below 0.5. However, if we are scoring Impact, either implicitly or explicitly, this rule would seem inappropriate. The rule makes many small sub-arguments, like the one about Roanoke airport, stop having any value. Perhaps the Roanoke airport argument alone is negligible but it still has a positive impact and, when added to all the other similar projects around the country, would amount to a sizeable contribution. Therefore it wouldn't be correct to nullify it altogether. |
|||
We also wouldn't want arguments from Impact to prematurely influence necessary [[Rhetorical argument|rhetorical argument]]s. Let's take a favorite from moral philosophy, that of a healthy young person, John who comes in for a routine checkup at a clinic which has 5 critical patients in need of organ transplants. John has the organs they need and is a match for all of them. The doctors, using a purely utilitarian argument decide to kill John and harvest his organs. It makes sense: 1 person dies and 5 live so we're ahead. Let's for the moment disregard legal and other social artifacts which might persuade the doctors otherwise. This approach contrasts with a deontological perspective which argues that the ends do not justify the means and that, indeed, the means in this case are all important. But we can only ferret out the deontological argument by actually having it, within the context of a rhetorical debate. We would hope such a debate would successfully preclude any utilitarian considerations whatsoever. |
|||
This leads us to the more general reason why separating the scoring techniques is appropriate. A score for Impact is essentially a [[Cost-benefit-risk analysis|cost-benefit-risk analysis]] for which established techniques exist and which would be confusing if scored together with the rhetorical argument. Indeed, by the time we reach an argument where impact is of interest we have usually dispensed with the rhetorical nature of the argument: |
|||
<kroki lang="graphviz"> |
|||
digraph G { |
|||
fontname="Helvetica,Arial,sans-serif" |
|||
node [fontname="Helvetica,Arial,sans-serif"] |
|||
edge [fontname="Helvetica,Arial,sans-serif"] |
|||
layout=dot |
|||
0 [label="0, Thesis: We have $150 billion to spend and \n should spend it on climate change"] |
|||
1 [label="1, Electric cars and charging stations.\n I = 0.5"] |
|||
2 [label="2, Home and building insulation, solar, heat pumps, etc.\n I = 0.3"] |
|||
3 [label="3, Carbon capture.\n I = 0.2"] |
|||
0 -> 1 [dir="forward"]; |
|||
0 -> 2 [dir="forward"]; |
|||
0 -> 3 [dir="forward"]; |
|||
} |
|||
</kroki> |
|||
We can see that this argument is likely the outcome of previous arguments where basic points have been agreed to (or at least settled) such as whether climate change is real, Biden is a good president, etc. Here we are at the final stages of the argument, which consists of a resolution to move forward with some practical course of action. |
|||
In this case each sub-argument is, in effect, a lobbying effort for the money. All the sub-arguments are equal in terms of their Veracity, rhetorical Relevance, freedom from Fallacies, and Clarity. The only point of dispute is whether the money is better spent on one option or another. In a situation like this, <math>\sum I = 1</math> would be defined as the effect of all plausible infrastructural investments we could make to impact climate change. In this respect let's assume we are limited to the three options above. The voters, presumably armed with engineering studies, would then weigh in to assess the impact of each proposal. |
|||
It is important to emphasize that the argument at this point is a technical one. It is numerical in nature and hinges on scientific rigor. Our system for assessing trust in the people who can reasonably provide input at this level will be important. One can easily imagine how interested parties (and the merely ignorant) could skew the results with their vote. At the same time we want to encourage participants to move toward this type of debate since it leads to practical benefits and, by its nature, tends to reduce partisan rancor. |
|||
The idea outlined here stands apart, by design, from the method that scores the rhetorical quality (eg the VRFC equation) of the argument. Rhetoric is designed to convince you of the argument as a whole but arguments using Impact are designed to forward a specific recommendation. Clearly, bundling the Impact with the VRFC equation is inappropriate. |
|||
In many cases arguments will have a hard time getting to this level of practicality. They tend to remain mired in the basic rhetoric that governs them: |
|||
<kroki lang="graphviz"> |
|||
digraph G { |
|||
fontname="Helvetica,Arial,sans-serif" |
|||
node [fontname="Helvetica,Arial,sans-serif"] |
|||
edge [fontname="Helvetica,Arial,sans-serif"] |
|||
layout=dot |
|||
0 [label="0, Thesis: Does God exist?"] |
|||
1 [label="1, Yes, because I can speak to Him and \n He responds by doing good things for me."] |
|||
2 [label="2, No, because there is no objective \n evidence that there is anyone listening."] |
|||
0 -> 1 [dir="forward"]; |
|||
0 -> 2 [dir="forward"]; |
|||
} |
|||
</kroki> |
|||
This argument is clearly truncated but we can see where it is going. It is, in essence, one about the Veracity of personal experience vs. demonstrable evidence, which is a philosophical debate. It is hard to ascribe Impact to it because it doesn't ever get to the point of enumerating proposals. |
|||
But it could eventually transform itself into one that did. Let's assume the participants agree to settle, or at least table, the philosophical debate and concentrate instead on a test of how to improve your life. Both the religious and secular sides propose certain practices: |
|||
<kroki lang="graphviz"> |
|||
digraph G { |
|||
fontname="Helvetica,Arial,sans-serif" |
|||
node [fontname="Helvetica,Arial,sans-serif"] |
|||
edge [fontname="Helvetica,Arial,sans-serif"] |
|||
layout=dot |
|||
0 [label="0, Thesis: Does God exist?"] |
|||
1 [label="1, Yes, because I can speak to Him and \n He responds by doing good things for me."] |
|||
2 [label="2, No, because there is no objective \n evidence that there is anyone listening"] |
|||
3 [label="3 ...more debate..."] |
|||
4 [label="4 ...more debate..."] |
|||
5 [label="5, Modified Thesis: Is your life best improved by religious or secular practices?"] |
|||
6 [label="6, Religious"] |
|||
7 [label="7, Secular"] |
|||
8 [label="8, Pray for 20 minutes \n every night and ask \n for what you need."] |
|||
9 [label="9, Go to your religious \n service every week and \n perform the rituals."] |
|||
10 [label="10, Study for 20 minutes \n every night in an area \n where your problems are."] |
|||
11 [label="11, Find a support group \n and meet with them \n every week."] |
|||
0 -> 1 [dir="forward"]; |
|||
0 -> 2 [dir="forward"]; |
|||
1 -> 3 [dir="forward"]; |
|||
2 -> 4 [dir="forward"]; |
|||
3 -> 5 [dir="forward"]; |
|||
4 -> 5 [dir="forward"]; |
|||
5 -> 6 [dir="forward"]; |
|||
5 -> 7 [dir="forward"]; |
|||
6 -> 8 [dir="forward"]; |
|||
6 -> 9 [dir="forward"]; |
|||
7 -> 10 [dir="forward"]; |
|||
7 -> 11 [dir="forward"]; |
|||
} |
|||
</kroki> |
|||
In this case, the reader is being invited to try the techniques on offer and an evaluation of Impact might thus be made. Note that in this case we have suspended our evaluation of the rhetorical qualities of each argument and begun a new one which seeks a utilitarian appraisal of which side might offer a better personal outcome. This is in keeping with the notion of Impact as separate from the rhetorical qualities of the argument. |
|||
We could, in theory, envision someone who is not religious adopting religious practices because he concludes that it does him good. Perhaps he tried both sides and decided the religious side was the one yielding the greatest benefit. This possibility is no doubt one motivation for religious debaters to drop their metaphysical convictions and adopt a practical way to approach their disagreement with the secular side. In any event, this progression seems like a healthy outcome since metaphysical debates usually have little hope of resolution. |
|||
Impact is necessarily focused on some particular goal. If the goal is material benefit and you pray and get rich you might think prayer works. But if the goal is broader than that, you might be disturbed by the fact that you are doing something you don't really believe is true. Your goal might be to get rich without compromising philosophical integrity. In this case the object of our Impact changes to become more than simply material wealth. A clear statement of the argument thesis in terms of goals is obviously important here. |
|||
In spite of our attempts at separating impact from rhetoric we will often find ourselves with a mix of the two: |
|||
[[File:Procon.png|center|frame]] |
|||
Here we've scored the Pro argument weaker than the Con argument using our standard rhetorical measures (VRFC). Arguably the Pro argument speculates more (a type of fallacy) about what would happen if we stopped supporting Ukraine. The Con argument isn't perfect either since it seems to assume that the money saved would actually be used in some constructive way. Still, money not spent is certainly money saved so we'll mark it down only slightly. That said, it would be ridiculous to stop the argument after concluding the Con side "won". The argument is not really a rhetorical argument at all but rather a statement of Impact. One side argues for the impact of saving the money. The other argues for the impact of failing to spend the money. We may not know how events would play out in this situation but we acknowledge the risk of catastrophic consequences for failure to act. The impact score for the Pro side is thus much higher. |
|||
This is a particular case where the argument should be separated out into one that is explicitly about impact but it is not clear how best to achieve that. One way would be to allow participants to intervene by asking questions or proposing to move the debate in a more fruitful direction, perhaps by suggesting a new main contention (ie thesis). |
|||
[[File:Procon2.png|center|frame]] |
|||
A basically new debate ensues. Incentives to move the debate might include reputational points for agreeing on a more productive direction. |
|||
Let's look at an example of what this "productive" argument might look like in terms of cost-benefit-risk analysis: |
|||
[[File:Productiveargument.png|center|frame]] |
|||
The red boxes are Con arguments and the green box is the Pro argument. We can see right away why the Pro argument might have stiff opposition since it leads to an infinite cost-benefit ratio and is virtually certain to occur (it is our current policy). It is possible that other scenarios could play out within the context of supporting Ukraine but let's leave these aside for the moment. |
|||
So the Pro side looks bad until we start looking at the Con scenarios. In Scenario 1 we envision taking the $75 billion spent on Ukraine aid and providing free [[community]] college instead. Doing so provides an economic benefit in the long run so we provide an estimate for that. However, military and policy experts have said that ignoring Ukraine would result in having to contain a newly resurgent Russia and this could double our defense costs in the near term ($800 billion). The resulting cost benefit ratio is 2.9, a positive number which is undesirable. It also is the highest probability scenario, at 70%. Other scenarios involve some type of war with Russia and would involve an even greater outlay of funds, not to mention the sheer human toll of war. Only Scenario 4 envisions a minor outlay to contain a victorious Russia which would be offset by the benefit of free community college. This scenario is desirable but unlikely. |
|||
These scenarios are much like sub-arguments but stripped of any need to assess their rhetorical quality. By looking at CB ratios and probabilities we can determine which policy direction to take. |
|||
<h3>Interaction effects between arguments and sub-arguments</h3> |
|||
Slashdot offers a system for content moderation summarized by the following from [Wikipedia](https://en.wikipedia.org/wiki/Slashdot): |
|||
Although arguments have been presented as standalone entities, users may often score them after reading, and accounting for, their sub-arguments. In that case, the sub-argument's influence on the parent argument would be counted twice -- once due to the mathematical effect discussed [[#Scoring of individual arguments|above]] and twice due to the the influence the sub-argument has on the user's scoring of the parent argument. |
|||
> Slashdot's editors are primarily responsible for selecting and editing the primary stories that are posted daily by submitters. The editors provide a one-paragraph summary for each story and a link to an external website where the story originated. Each story becomes the topic for a threaded discussion among the site's users.[62] A user-based moderation system is employed to filter out abusive or offensive comments.[63] Every comment is initially given a score of −1 to +2, with a default score of +1 for registered users, 0 for anonymous users (Anonymous Coward), +2 for users with high "karma", or −1 for users with low "karma". As moderators read comments attached to articles, they click to moderate the comment, either up (+1) or down (−1). Moderators may choose to attach a particular descriptor to the comments as well, such as "normal", "offtopic", "flamebait", "troll", "redundant", "insightful", "interesting", "informative", "funny", "overrated", or "underrated", with each corresponding to a −1 or +1 rating. So a comment may be seen to have a rating of "+1 insightful" or "−1 troll".[57] Comments are very rarely deleted, even if they contain hateful remarks.[64][65] |
|||
This effect is clearly undesirable and efforts should be made to control it. The software could, for instance, be equipped with the following checks: |
|||
> Starting in August 2019 anonymous comments and postings have been disabled. |
|||
* If it detects that a user voted for a sub-argument and subsequently voted for an argument, it can flag the sub-argument score so it does not participate in the mathematical effect it would otherwise have on the argument. We are assuming here, of course, that a user who has voted for a sub-argument will be unable to avoid having it influence his vote for the parent argument. |
|||
> Moderation points add to a user's rating, which is known as "karma" on Slashdot. Users with high "karma" are eligible to become moderators themselves. The system does not promote regular users as "moderators" and instead assigns five moderation points at a time to users based on the number of comments they have entered in the system – once a user's moderation points are used up, they can no longer moderate articles (though they can be assigned more moderation points at a later date). Paid staff editors have an unlimited number of moderation points.[57][62][66] A given comment can have any integer score from −1 to +5, and registered users of Slashdot can set a personal threshold so that no comments with a lesser score are displayed.[62][66] For instance, a user reading Slashdot at level +5 will only see the highest rated comments, while a user reading at level −1 will see a more "unfiltered, anarchic version".[57] A meta-moderation system was implemented on September 7, 1999,[67] to moderate the moderators and help contain abuses in the moderation system.[68][unreliable source?][page needed] Meta-moderators are presented with a set of moderations that they may rate as either fair or unfair. For each moderation, the meta-moderator sees the original comment and the reason assigned by the moderator (e.g. troll, funny), and the meta-moderator can click to see the context of comments surrounding the one that was moderated.[62][66] |
|||
* If it detects a vote for an argument but not a vote for its sub-argument, it doesn't know if the user has read the sub-argument in a way that would influence their vote for the parent argument. In such a case, the user can simply be asked if the sub-argument was read and, if so, to flag any subsequent vote by the user for the sub-argument as a non-participant in its mathematical influence on the parent argument. |
|||
* If the sub-argument does not yet exist when the vote for the parent argument is cast, the software will flag a subsequent vote for any newly developed sub-argument as a legitimate participant in the mathematical influence it has on the parent argument. |
|||
It is probably difficult to make a system like this foolproof. A user might report not having read a sub-argument that they have, in fact, read. Tracking features could, in theory, be developed to check whether this is the case and react accordingly. However, it would still be difficult to know for sure how deeply the user understands the sub-argument just based on a record that they clicked on it or had it "open". It also seems like it would be easy to overdo tracking of this kind to the point where it simply turns off an otherwise enthusiastic user. Another interesting idea is the use of word descriptors to match scores. In our system descriptors such as "Completely irrelevant", "somewhat irrelevant", etc. could be a useful way to break up corresponding numerical ranges in our 0-1 scoring system. |
|||
Latest revision as of 21:03, 26 September 2024
Some thoughts on evaluating arguments
Here we discuss how we might evaluate an argument made by a respondent instead of simply relying on the given probability (as we've been doing so far). An argument, assuming it is made public, could then be evaluated by the questioner and others independently to find a more accurate probability. This opens up a new idea in our work, that of assessing the truth by evaluating the reasoning put forth in an opinion.
One idea for doing this starts with a simple model for argument construction. The argument consists of supporting statements which are tied together with logic to form a conclusion. The conclusion is the answer to the overall question being asked of the network. Each supporting statement and the logic can be evaluated independently to determine the extent to which the conclusion is true. The following diagram illustrates this:
The probability of the supporting statements can be combined in a Bayesian manner. This is in keeping with the Bayesian idea of modifying prior probabilities given new evidence (ie supporting statements). These probabilities can be trust-modified as Sapienza proposed (https://ceur-ws.org/Vol-1664/w9.pdf) but since they are likely being assigned by the questioner, we will assume that trust is already built into them. Of more importance is the relevance of the supporting statements. They can range from completely irrelevant to completely relevant. A completely relevant statement will take the full value of the probability it was originally assigned. A completely irrelevant statement would reduce the probability to 50%, where it will have no influence on the outcome. In that sense relevance functions in the same way trust does to modify the probability:
where
is relevance (0.0 - 1.0)
is relevance-modified probability
is the nominal probability (=0.5 for a predicate question)
is the unmodified probability
After the relevance-modification, each supporting statement is combined in the usual manner via Bayes. For the first two statements,
and so on for each additional statement. Here it is to be understood that , etc. is the value after the relevance modification.
Logic will also have a probability assigned to it to represent its quality. A fully illogical argument would receive a 0, which when combined via Bayes with the supporting statements would render the probability of the entire argument 0. This makes sense because a completely illogical argument, regardless of the strength of its supporting statements, destroys itself. A fully logical argument, however, will not receive a 1 but rather a 0.5. When combined with the supporting statements a 1 would render the final probability a 1, which is not reasonable. A 0.5, however, would do nothing and the final probability would be the combined probability of the supporting statements. Thus we assume that perfect logic is neutral and less than perfect logic reduces the combined probability of the statements. Again, this seems reasonable. We expect, by default, logical arguments which then rest on the strength of their supporting statements. If we notice flaws in the logic we discount the strength of the argument accordingly.
Let's try an example with these ideas:
Question: Are humans causing frog populations to decline?
Answer / Conclusion: Yes, mankind is causing a fall in frog populations.
Logic: Mankind is causing the fall of frog populations if we can show that frog populations are decreasing over time and can show a human behavior that causes the decline.
Supporting Statements:
- Frog populations have declined since the 1950's.
- My wife complained that she doesn't see frogs anymore.
- Scientists say that the loss of freshwater habitats has affected frog populations.
We start by judging the quality of the supporting statements. 1 seems like a well substantiated statement (a high P) but is not completely relevant because it only hints at human involvement. 2 is completely true but mostly irrelevant. 3 is a contributor but seems less substantiated than 1 and contains no human cause. We proceed by assigning probability and relevance values:
Since s2 won't count in the Bayesian calculation we can ignore it and:
The logic/conclusion in this case is reasonably strong so we will assign it a high value, say (remember, out of 0.5). It could be improved by observing that the word "behavior" is too general and should be replaced by, say, "policy choice" (ie urban growth into ecologically important wetlands). We note here that logic is more than just the mathematical construction of an argument. Since we are speaking a human language, logic might also be flawed because it uses imprecise wording.
Putting together with using Bayes we obtain a concluding probability:
One potential pitfall of this model is that repetitive supporting statements of high probability will quickly render a combined probability near 1.0. As we've seen in the past, this is simply the result of the Bayes equation. The user would need to watch for attempts like these to distort the answer by removing repetitive statements or making them irrelevant.
Scoring of individual arguments
Arguments can be scored on veracity, impact, relevance, clarity, and informal quality (lack of fallacies):
- Veracity is how true the argument is based on source information. Source information itself will be scored:
- Impact & Relevance is how deeply the argument affects the main contention of the debate (or the argument immediately above):
- Clarity is how understandable the argument is:
- Informal quality (lack of fallacies) is whether the argument commits any logical fallacies of its own. A list of informal fallacies (and formal ones) will be provided to help users select appropriately:
Since Impact and Relevance are closely related concepts we will merge these into one, Relevance. The simplest method for combining these is to average them, or weighted average them:
where
is a weighting for category X (eg Veracity, Relevance, etc)
This seems reasonable and if we believe that certain criteria should weigh more (such as Veracity) we can easily make the weighting factors reflect this. However, intuitively it seems that a category such as Veracity should not only weigh more but have the power to take down the whole argument. After all, if the argument is a straightforward lie, it should receive a score of zero, regardless of its other attributes (such as relevance, clarity, etc):
Who is the best choice for President? X is the best choice because he will land a person on Mars in his first year.
This argument is a lie and although it is clear, has no evident fallacies, and is relevant to the question at hand, it should be thrown out.
The same can be said of Relevance. A completely irrelevant argument should also have the power to render the whole argument moot:
Who is the best choice for President? X is the best choice because he likes pizza and so do I.
With this in mind, we can propose the following equation, which we will dub the "VRFC equation":
Where
= Score for the argument which varies from 0-1
= weighting factor for Fallacies.
= weighting factor for Clarity.
and each of the constituent variables () has a range 0-1.
In this equation either Veracity or Relevance have the power to nullify the entire argument. Similarly a combination of Fallacies and lack of Clarity can do the same. However, a fallacious argument alone seems like it could still have merit, as would an argument whose only flaw was lack of clarity:
We should support Czechoslovakia because if the Nazi's prevail they will conquer the world.
This argument commits the slippery slope fallacy but is not entirely invalid. Similarly an unclear argument can still manage to make a point:
We should support Europe because first the Sudetenland, then the Czechs, and soon enough it's over when all the Brits had to do was get rid of that weakling sooner.
It would seem that a fallacious argument should weigh more than an unclear one. Proposed weights might be:
Rolling up the score of argument trees
The equation above applies to a single argument but, as we've seen, most arguments have sub-arguments below, sub-sub-arguments, and so forth. They are really trees in which each individual argument can be scored separately.
Here we develop a proposed equation for rolling up the score for an argument based on its own score and that of its sub-arguments. In doing so we emphasize that any argument can stand on its own and be scored in the absence of sub-arguments. This creates an interesting dynamic. The sub-argument may bolster or detract from the parent argument but the extent to which it does should be limited.
Furthermore, once the sub-argument becomes weaker than a certain threshold, it should stop influencing the parent argument altogether. Here, we will set this threshold at 0.5. Thus only Pro sub-arguments that score 0.5 or better will have any influence on the parent argument. For Con sub-arguments we will use the same threshold but first modify the sub-argument score by . Thus a strong Con sub-argument, scoring say 0.9, would enter the calculation with a score of 0.1. The result is a range of scores 0-1 of which 0-0.5 is Con and 0.5-1 is Pro. Scores of exactly 0.5 are neutral.
Let's consider the case with one argument and one pro sub-argument and one Con sub-argument.
In this case the argument's score is 0.9, and both the Pro/Con sub-argument score is 0.7. These numbers would normally be arrived at by using the VRFC eqn above, but we will just assume them for now. The first sub-argument, in this case, bolsters the argument because it is a Pro argument and has a score (0.7) greater than 0.5. The second sub-argument, with the same score, detracts from the argument because it is on the Con side. We emphasize that if these scores were at or below 0.5 they would have no effect on the argument.
The general equation governing this situation is as follows:
For and
For and
For and </math>x > 0.5</math>
For and
where
= score for parent argument
= score for Pro arguments
= score for Con arguments
= maximum possible fraction of increase possible, 0-1
The variable is a user selected number between 0-1 and represents the extent to which the sub-argument score can be affected. For example, a sub-argument with x = 0.9, as in the diagram above, can be improved by 0.1 to a maximum of 1. Then represents the fraction of 0.1 that we will allow for our improvement. If , for instance, then the maximum range around 0.9 that the sub-argument can affect is . Thus the maximum score the argument can have is 0.925 and the minimum is 0.875.
For the argument above:
User input
For the Pro sub-argument:
For the Con sub-argument:
We can see here that the Pro and Con sub-arguments exactly balance each other since they both have the same score.
The equation above is piecewise linear and can be visualized as follows:

One important property of this equation is that the stronger (or weaker) an argument becomes, it becomes harder for a sub-argument to change it. This is because the maximum allowed movement is if or simply if . The idea behind this property is that very strong arguments should be harder to dislodge precisely because they have covered themselves well. A weaker argument, for instance one that fails to mention an obvious supporting fact, is in a position to be bolstered more by a sub-argument which mentions the fact. Similarly a very weak argument should be difficult to bolster. If the argument is a lie or irrelevant, for instance, there isn't much that can be done to rescue it.
This property has the further consequence that cannot be changed by the sub-arguments if it is 1 or 0. A truly perfect argument, , cannot be weakened no matter how strong its Con sub-argument. Similarly a perfectly flawed argument, cannot be bolstered with any Pro sub-argument. We will discuss below a method to deal with the fact that, regardless of the quality of the argument, users may still vote to score arguments 1 or 0.
Population adjustments
The algorithm described above assumes a single vote for the argument and sub-arguments. In fact, this will rarely be the case, because multiple users will be voting on each. The effect of a sub-argument on its parent should be weighed by the population of users who voted for the sub-argument and parent argument.
Here we propose a simple modification factor, based on the ratio of users voting for each argument/sub-argument:
where
is the population modified score
is the modified score without population modifications (see above)
is the population voting for the sub-argument
is the population voting for the parent argument
is the original score of the parent argument
Usually we expect that sub-arguments will receive fewer votes than parent arguments, so in general. For the case when we will force . Therefore there is no danger that a sub-argument can overwhelm a parent argument by voting power alone. This is in keeping with our philosophy that sub-arguments can have at best a limited effect on parent arguments.
Example calculation
Let's do a problem with the following argument tree and :
Our objective here is to roll up the score for the Pro side of this tree. The Con side would be calculated similarly and we will skip this for the sake of brevity. Note that stands for the score and is the population voting to produce that score. We start at the bottom, with the 2-3-4 portion of the tree, and for the sake of consistency with the above calculation we will recast for 2 as and label the population of the sub-arguments as .
For the Pro sub-argument, we write:
We modify this by the respective populations:
For the Con sub-argument we first modify its score,
and write
and modify by the respective population,
These two values of can now be combined to create a new for the Pro argument:
We note here that the Pro argument got a little stronger as a result of its sub-arguments. The Pro sub-argument was substantially stronger than the Con sub-argument and, although fewer people voted for it, the population difference was not large.
For the Con sub-argument 5-6-7 we have the following situation:
Here, for the Pro sub-argument, we first modify its score since it is the opposite of its parent. It is as if the parent were a Pro argument and the child were a Con argument.
We then proceed as usual with the calculation:
For the Con sub-argument since the parent argument is also Con:
We combine these two results in the same manner as above:
With the bottom layer of the tree calculated, we have the following situation:
All that remains is to calculate the 1-2-5 portion, which is very similar to the 2-3-4 calculation performed above. Therefore will skip the details of this and simply report the results:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{mod, tot} = 0.901}
We see here that the final result is not much different than the original Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = 0.9} . This is a result of the Pro sub-arguments essentially being cancelled by the Con sub-arguments. Such a result is to be expected in many cases.
In this example, we are skipping the Con side of the overall argument (node 8 in the tree above) because it would be exactly the same as what we have shown. If it had been calculated we would then combine the result for 1 and 8 to produce an overall score for the argument.
The calculations above can be performed with the [attached snippet](https://gitlab.syncad.com/peerverity/trust-model-playground/-/snippets/164). The user input portion of the snippet is set up for the calculation we did immediately above:
#User input
side_parent = 'pro' #side, pro or con, that the parent argument is on
s = 0.9 #score for the parent argument
mf = 0.25 #max fraction that parent argument can be changed in terms of (1-s) or (s-0)
p = 96.0 #population voting for the parent argument
x_pro_arr = [0.713] #score for the pro children
x_con_arr = [0.721] #score for the con children
ps_pro_arr = [55.0] #population voting for each pro child sub-argument
ps_con_arr = [43.0] #pop voting for each con child sub-argument
mods_if1or0 = True #True if we want scores of 1 or 0 to be modified to near 1 or 0 (otherwise they can't be adjusted by this calculation)
To note, the snippet contains arrays to handle any number of child arguments. These are combined in the same way we combined the single Pro and Con argument above.
Another variable, `mods_if1or0` controls whether we allow Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} to be modified when it is set to 1 or 0. As discussed above, arguments where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = 1} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = 0} are perfect, or perfectly flawed, and thus cannot be changed with sub-arguments. This idea may be theoretically plausible but it wouldn't stop users from voting 1 or 0 for arguments. In such cases the `mods_if1or0` switch, when True, changes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} to 0.99 and 0.01 respectively.
As a side note, this property is similar to Bayesian probabilities of 1 or 0 which also cannot be changed. We have discussed this problem in earlier posts under the guise that 1 or 0 probabilities don't really exist because they would require an infinite sample size. In the same way, a perfect argument (or perfectly imperfect) argument cannot exist because it would, at some point, run into the same issues that Bayesian probabilities do.
For example, suppose we've invented a pill that cures cancer. It is one dose, costs 10 cents to make, has no side effects, has no environmental impact due to manufacture, and is certain to cure someone's cancer. The argument for a cancer patient taking the pill is, for all practical purposes, perfect. There is simply no plausible argument against it. We could score such an argument a 1 until we remember our probabilities. We only know the pill works and has no side effects on a limited population, say 100,000 patients. We don't know what effect it will have on the 100,001st patient. So the best we can say is that the drug is 0.99999 effective. Given that the argument is really predicated on the effectiveness of the drug we could say its score is also 0.99999.
Slashdot
Slashdot offers a system for content moderation summarized by the following from [wikipedia:Slashot|wikipedia]:
- Slashdot's editors are primarily responsible for selecting and editing the primary stories that are posted daily by submitters. The editors provide a one-paragraph summary for each story and a link to an external website where the story originated. Each story becomes the topic for a threaded discussion among the site's users. A user-based moderation system is employed to filter out abusive or offensive comments.[63] Every comment is initially given a score of −1 to +2, with a default score of +1 for registered users, 0 for anonymous users (Anonymous Coward), +2 for users with high "karma", or −1 for users with low "karma". As moderators read comments attached to articles, they click to moderate the comment, either up (+1) or down (−1). Moderators may choose to attach a particular descriptor to the comments as well, such as "normal", "offtopic", "flamebait", "troll", "redundant", "insightful", "interesting", "informative", "funny", "overrated", or "underrated", with each corresponding to a −1 or +1 rating. So a comment may be seen to have a rating of "+1 insightful" or "−1 troll".[57] Comments are very rarely deleted, even if they contain hateful remarks.
- Starting in August 2019 anonymous comments and postings have been disabled.
- Moderation points add to a user's rating, which is known as "karma" on Slashdot. Users with high "karma" are eligible to become moderators themselves. The system does not promote regular users as "moderators" and instead assigns five moderation points at a time to users based on the number of comments they have entered in the system – once a user's moderation points are used up, they can no longer moderate articles (though they can be assigned more moderation points at a later date). Paid staff editors have an unlimited number of moderation points. A given comment can have any integer score from −1 to +5, and registered users of Slashdot can set a personal threshold so that no comments with a lesser score are displayed. For instance, a user reading Slashdot at level +5 will only see the highest rated comments, while a user reading at level −1 will see a more "unfiltered, anarchic version". A meta-moderation system was implemented on September 7, 1999,to moderate the moderators and help contain abuses in the moderation system. Meta-moderators are presented with a set of moderations that they may rate as either fair or unfair. For each moderation, the meta-moderator sees the original comment and the reason assigned by the moderator (e.g. troll, funny), and the meta-moderator can click to see the context of comments surrounding the one that was moderated.
Slashdot's purpose is to promote high quality discussion which is somewhat similar to our purpose of promoting high quality arguments. In particular, the reputation (karma) of the moderators is an interesting concept. We could use a similar system to weight voters with a good reputation higher in their argument scoring. Another interesting idea is the use of word descriptors to match scores. In our system descriptors such as "Completely irrelevant", "somewhat irrelevant", etc. could be a useful way to break up corresponding numerical ranges in our 0-1 scoring system.
Refining our Argument Score with Reputation/Trust
Above we discussed an equation to score arguments on the basis of Veracity, Relevance, Freedom from Fallacies, and Clarity:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = VR(w_fF + w_cC) }
Where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is overall score
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is Veracity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is Relevance
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} is Fallacies (ie freedom from fallacies)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is Clarity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_f} is weighting for Fallacies, eg 0.7
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_c} is weighting for Clarity, eg 0.3
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_f + w_c = 1}
Each user would vote on each category and the resulting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
would be calculated. However, each user may have a different reputation/trust for their ability to judge these four criteria. We can take this into account by simply adding a weighting factor for Trust:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = (T_vV)(T_rR)(w_fT_fF + w_cT_cC) }
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_x} = Trust in user's ability to evaluate each category Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} (Veracity, Relevance, Fallacies, and Clarity)
Since the user evaluates trust in multiple categories, it would be useful to generate a composite trust for all the categories:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{comp} = {(T_vV)(T_rR)(w_fT_fF + w_cT_cC) \over{VR(w_fF + w_cC)}} }
Where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{comp}} is the composite trust for all categories.
Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{comp}} can also be seen as an "average" trust, ie the single factor that produces the same argument score as that resulting from the multiple trust factors.
Once we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{comp}} we can use it to generate an average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} for all users:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{ave} = {\sum S \over{\sum T_{comp}}} }
That is, instead of dividing by the number of people voting, we divide by the total of how much they "count". This is similar to the [trust-weighted average scheme](A trust weighted averaging technique to supplement straight averaging and Bayes) we have proposed before. It is this average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} that we will take to be the score for the argument.
Rhetorical vs. Practical Arguments
So far our scoring methodology has been focused mainly on rhetorical aspects of arguments. Is the argument true, relevant to its parent contention, clear, and logical? These criteria certainly touch on the practical impact an argument may have and so far we have been merging Impact with Relevance since it is hard to distinguish the two. Consider the following:
Here it would seem appropriate to roll Impact into Relevance. Presumably most voters will recognize Sub-argument 2 as being the more relevant one simply because it is, on a practical level, the more impactful one.
However, usually Relevance is a rhetorical quality, not a practical one. In this case, as a matter of rhetoric, both supporting arguments are relevant to the topic at hand. They are both, without question, part of Biden's infrastructure bill. They are both true, clear, and free of fallacies. But even so, although it is clear what is going on, it would be better to separate the issue of whether Biden is a good president from the issue of which infrastructure allocations add the most value.
One reason for this separation, in terms of the [math laid out previously](Argument scoring), is that a weak sub-argument stops having any influence once its score goes below 0.5. However, if we are scoring Impact, either implicitly or explicitly, this rule would seem inappropriate. The rule makes many small sub-arguments, like the one about Roanoke airport, stop having any value. Perhaps the Roanoke airport argument alone is negligible but it still has a positive impact and, when added to all the other similar projects around the country, would amount to a sizeable contribution. Therefore it wouldn't be correct to nullify it altogether.
We also wouldn't want arguments from Impact to prematurely influence necessary rhetorical arguments. Let's take a favorite from moral philosophy, that of a healthy young person, John who comes in for a routine checkup at a clinic which has 5 critical patients in need of organ transplants. John has the organs they need and is a match for all of them. The doctors, using a purely utilitarian argument decide to kill John and harvest his organs. It makes sense: 1 person dies and 5 live so we're ahead. Let's for the moment disregard legal and other social artifacts which might persuade the doctors otherwise. This approach contrasts with a deontological perspective which argues that the ends do not justify the means and that, indeed, the means in this case are all important. But we can only ferret out the deontological argument by actually having it, within the context of a rhetorical debate. We would hope such a debate would successfully preclude any utilitarian considerations whatsoever.
This leads us to the more general reason why separating the scoring techniques is appropriate. A score for Impact is essentially a cost-benefit-risk analysis for which established techniques exist and which would be confusing if scored together with the rhetorical argument. Indeed, by the time we reach an argument where impact is of interest we have usually dispensed with the rhetorical nature of the argument:
We can see that this argument is likely the outcome of previous arguments where basic points have been agreed to (or at least settled) such as whether climate change is real, Biden is a good president, etc. Here we are at the final stages of the argument, which consists of a resolution to move forward with some practical course of action.
In this case each sub-argument is, in effect, a lobbying effort for the money. All the sub-arguments are equal in terms of their Veracity, rhetorical Relevance, freedom from Fallacies, and Clarity. The only point of dispute is whether the money is better spent on one option or another. In a situation like this, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum I = 1} would be defined as the effect of all plausible infrastructural investments we could make to impact climate change. In this respect let's assume we are limited to the three options above. The voters, presumably armed with engineering studies, would then weigh in to assess the impact of each proposal.
It is important to emphasize that the argument at this point is a technical one. It is numerical in nature and hinges on scientific rigor. Our system for assessing trust in the people who can reasonably provide input at this level will be important. One can easily imagine how interested parties (and the merely ignorant) could skew the results with their vote. At the same time we want to encourage participants to move toward this type of debate since it leads to practical benefits and, by its nature, tends to reduce partisan rancor.
The idea outlined here stands apart, by design, from the method that scores the rhetorical quality (eg the VRFC equation) of the argument. Rhetoric is designed to convince you of the argument as a whole but arguments using Impact are designed to forward a specific recommendation. Clearly, bundling the Impact with the VRFC equation is inappropriate.
In many cases arguments will have a hard time getting to this level of practicality. They tend to remain mired in the basic rhetoric that governs them:
This argument is clearly truncated but we can see where it is going. It is, in essence, one about the Veracity of personal experience vs. demonstrable evidence, which is a philosophical debate. It is hard to ascribe Impact to it because it doesn't ever get to the point of enumerating proposals.
But it could eventually transform itself into one that did. Let's assume the participants agree to settle, or at least table, the philosophical debate and concentrate instead on a test of how to improve your life. Both the religious and secular sides propose certain practices:
In this case, the reader is being invited to try the techniques on offer and an evaluation of Impact might thus be made. Note that in this case we have suspended our evaluation of the rhetorical qualities of each argument and begun a new one which seeks a utilitarian appraisal of which side might offer a better personal outcome. This is in keeping with the notion of Impact as separate from the rhetorical qualities of the argument.
We could, in theory, envision someone who is not religious adopting religious practices because he concludes that it does him good. Perhaps he tried both sides and decided the religious side was the one yielding the greatest benefit. This possibility is no doubt one motivation for religious debaters to drop their metaphysical convictions and adopt a practical way to approach their disagreement with the secular side. In any event, this progression seems like a healthy outcome since metaphysical debates usually have little hope of resolution.
Impact is necessarily focused on some particular goal. If the goal is material benefit and you pray and get rich you might think prayer works. But if the goal is broader than that, you might be disturbed by the fact that you are doing something you don't really believe is true. Your goal might be to get rich without compromising philosophical integrity. In this case the object of our Impact changes to become more than simply material wealth. A clear statement of the argument thesis in terms of goals is obviously important here.
In spite of our attempts at separating impact from rhetoric we will often find ourselves with a mix of the two:
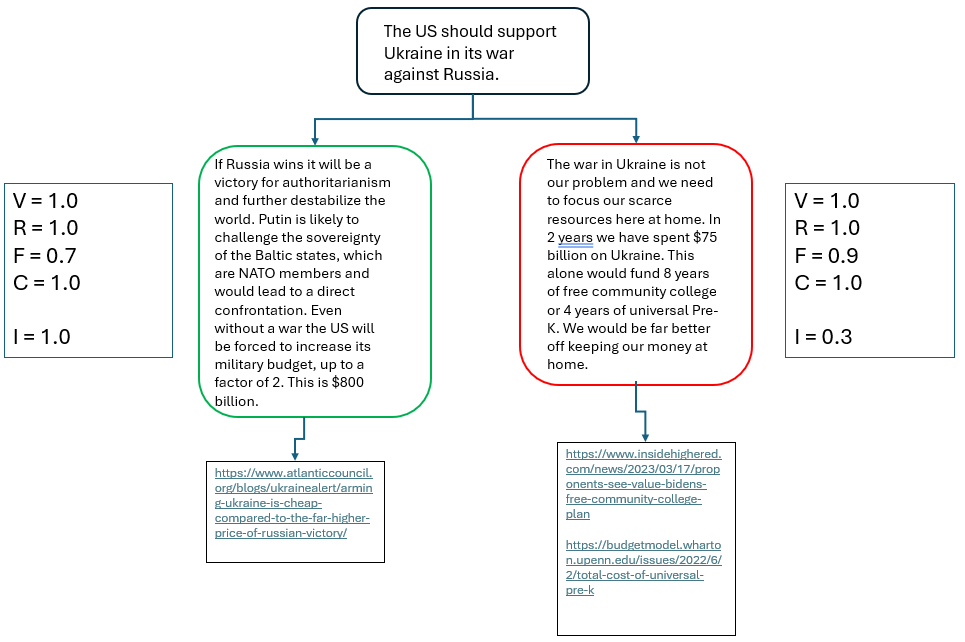
Here we've scored the Pro argument weaker than the Con argument using our standard rhetorical measures (VRFC). Arguably the Pro argument speculates more (a type of fallacy) about what would happen if we stopped supporting Ukraine. The Con argument isn't perfect either since it seems to assume that the money saved would actually be used in some constructive way. Still, money not spent is certainly money saved so we'll mark it down only slightly. That said, it would be ridiculous to stop the argument after concluding the Con side "won". The argument is not really a rhetorical argument at all but rather a statement of Impact. One side argues for the impact of saving the money. The other argues for the impact of failing to spend the money. We may not know how events would play out in this situation but we acknowledge the risk of catastrophic consequences for failure to act. The impact score for the Pro side is thus much higher.
This is a particular case where the argument should be separated out into one that is explicitly about impact but it is not clear how best to achieve that. One way would be to allow participants to intervene by asking questions or proposing to move the debate in a more fruitful direction, perhaps by suggesting a new main contention (ie thesis).
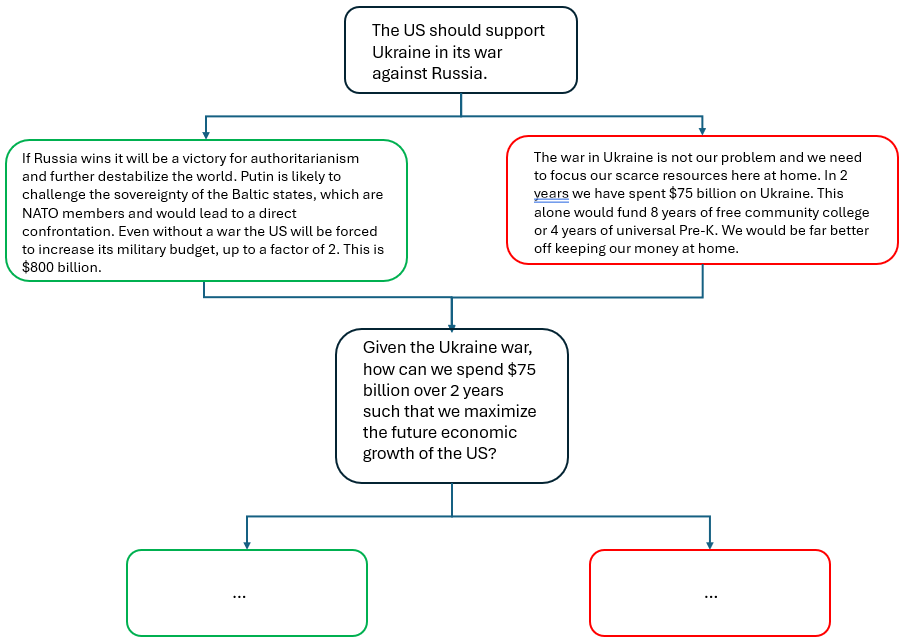
A basically new debate ensues. Incentives to move the debate might include reputational points for agreeing on a more productive direction.
Let's look at an example of what this "productive" argument might look like in terms of cost-benefit-risk analysis:
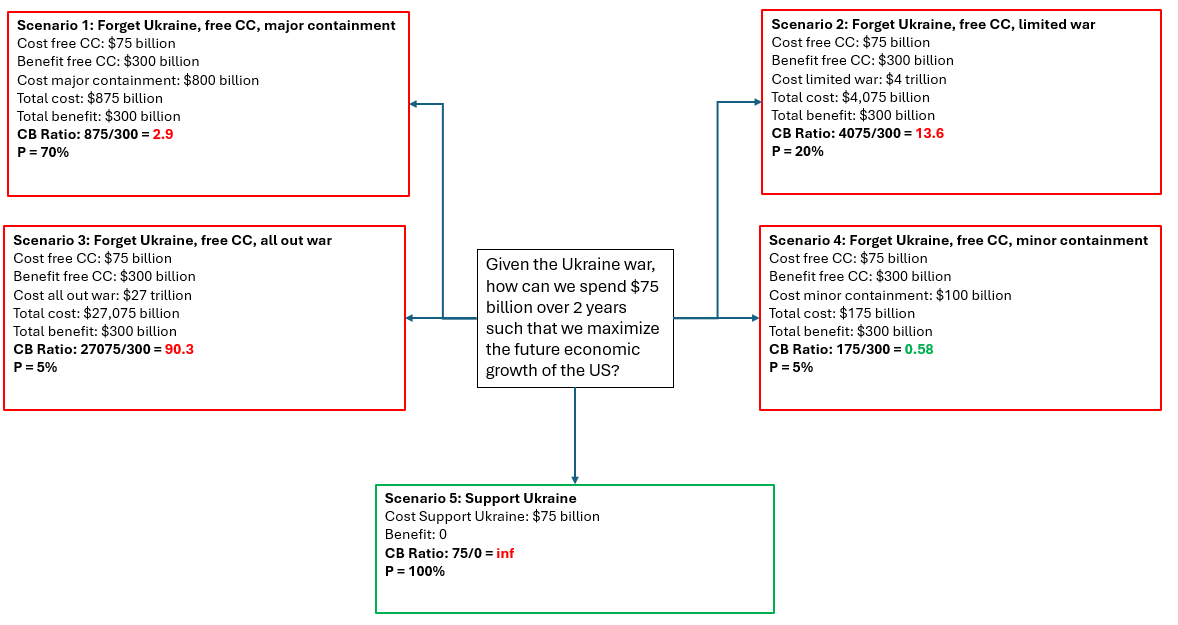
The red boxes are Con arguments and the green box is the Pro argument. We can see right away why the Pro argument might have stiff opposition since it leads to an infinite cost-benefit ratio and is virtually certain to occur (it is our current policy). It is possible that other scenarios could play out within the context of supporting Ukraine but let's leave these aside for the moment.
So the Pro side looks bad until we start looking at the Con scenarios. In Scenario 1 we envision taking the $75 billion spent on Ukraine aid and providing free community college instead. Doing so provides an economic benefit in the long run so we provide an estimate for that. However, military and policy experts have said that ignoring Ukraine would result in having to contain a newly resurgent Russia and this could double our defense costs in the near term ($800 billion). The resulting cost benefit ratio is 2.9, a positive number which is undesirable. It also is the highest probability scenario, at 70%. Other scenarios involve some type of war with Russia and would involve an even greater outlay of funds, not to mention the sheer human toll of war. Only Scenario 4 envisions a minor outlay to contain a victorious Russia which would be offset by the benefit of free community college. This scenario is desirable but unlikely.
These scenarios are much like sub-arguments but stripped of any need to assess their rhetorical quality. By looking at CB ratios and probabilities we can determine which policy direction to take.
Interaction effects between arguments and sub-arguments
Although arguments have been presented as standalone entities, users may often score them after reading, and accounting for, their sub-arguments. In that case, the sub-argument's influence on the parent argument would be counted twice -- once due to the mathematical effect discussed above and twice due to the the influence the sub-argument has on the user's scoring of the parent argument.
This effect is clearly undesirable and efforts should be made to control it. The software could, for instance, be equipped with the following checks:
- If it detects that a user voted for a sub-argument and subsequently voted for an argument, it can flag the sub-argument score so it does not participate in the mathematical effect it would otherwise have on the argument. We are assuming here, of course, that a user who has voted for a sub-argument will be unable to avoid having it influence his vote for the parent argument.
- If it detects a vote for an argument but not a vote for its sub-argument, it doesn't know if the user has read the sub-argument in a way that would influence their vote for the parent argument. In such a case, the user can simply be asked if the sub-argument was read and, if so, to flag any subsequent vote by the user for the sub-argument as a non-participant in its mathematical influence on the parent argument.
- If the sub-argument does not yet exist when the vote for the parent argument is cast, the software will flag a subsequent vote for any newly developed sub-argument as a legitimate participant in the mathematical influence it has on the parent argument.
It is probably difficult to make a system like this foolproof. A user might report not having read a sub-argument that they have, in fact, read. Tracking features could, in theory, be developed to check whether this is the case and react accordingly. However, it would still be difficult to know for sure how deeply the user understands the sub-argument just based on a record that they clicked on it or had it "open". It also seems like it would be easy to overdo tracking of this kind to the point where it simply turns off an otherwise enthusiastic user. Another interesting idea is the use of word descriptors to match scores. In our system descriptors such as "Completely irrelevant", "somewhat irrelevant", etc. could be a useful way to break up corresponding numerical ranges in our 0-1 scoring system.
















































































