Attenuation in trust networks

Main article: Technical overview of the ratings system

Review of Cycling

To summarize cycling briefly, if Trust=1.0 for all nodes, then cycling will rapidly lead to a confidence of 1 (100%) for a given question (if probabilities for most of the nodes are above 50%). However, if Trust < 1.0 then the confidence will asymptotically approach some limit below 1. The question was asked, why? Why the asymptote? I hadn’t, and still really haven’t, done the math to answer this (See APPENDIX below for an attempt) so I offered up the following qualitative explanation:

1. The confidence goes to 100% in a cycling network with Trust=1 (as long as our probabilities are above 50%). If Trust=0, the confidence is simply the confidence of the head node, which trusts itself. We would think that if Trust is between 0 and 1 that the confidence would also go to 100% if enough cycling were to take place, just like the case when Trust=1.0. But this would imply a sharp discontinuity between Trust=0 and everything else. Usually, when given a choice between continuous and discontinuous, you should pick continuous. Nature just seems to work that way, at least from a human-scale point of view. It is more reasonable that a continuous variation exists between Trust=0 and Trust=1.
2. The asymptote is the result of two forces fighting each other: one being the multiple counting of the same nodes over and over (cycling) and the other being the attenuation of the trust as the nodes get further away from the top-most node. When trust=1, no attenuation occurs so the full effect of multiple counting takes over. When Trust < 1, nodes further out exert less and less influence on the final answer because they have to go through multiple trust layers and, hence, become attenuated. A node with Trust=0 has no influence on the final answer which is almost the same as the influence a distant node has. Since its influence is almost nothing we could view that as being effectively the same as a trust of zero. Hence the term “trust attenuation”. As nodes get farther away from the top node their “effective” trust declines more and more.

Effect of Trust Attenuation

Let’s note first that this has nothing to do with cycling. Even in networks where no cycling takes place, if the trust of multiple nodes is below 1, attenuation will cause the last node to have very little influence on the final answer.

Let’s look at the implications of this. If a node that’s many levels down has low trust (due to attenuation) but is the only node that has any informed knowledge of a subject, how do we factor that in without completely washing out the information it provides? It seems a shame to discount the only node that knows anything because of attenuation.

Cases of this would be any question that is difficult to answer and will require an extensive dive into the network to find an authoritative source. In this situation most of the network doesn’t know anything but there’s one guy who does, somewhere deep down. Examples would be serious questions we might really pose: Is Bibi, from Israel, who just contacted me for a business deal, a good guy? Is it better to get a liver transplant in India or the US? No one in my immediate network knows the answer to these questions so it’s going to take a few levels to get there. The problem is that the network path to anyone who knows is long and has trust factors built in to every node which will attenuate the result as we go along. Take a look at the following example:

Here all nodes have a trust of 70% for their succeeding node and Nodes 0-7 have P=50%, meaning they don’t know anything and their contribution to the overall answer is nil. The only node with any real knowledge is 8, which we represent as P=100%. If we use sapienza_trusttree.py to compute this case we arrive at Ptot = 53% as shown. This is not a very good result, just slightly better than random.

Let’s contrast this with a network composed of two nodes, where there is a direct link between 0 and 8:

Here, by eliminating all the nodes that contribute nothing to the answer except attenuation, we obtain the far more reasonable result of 85%.

Ideas for Dealing with Trust Attenuation

To handle this we could allow the user to assign trust factors of 1 to nodes that don’t know the answer (ie ones that have 50% confidence). Trust seems like a less likely issue in cases where people simply don’t know but are willing to pass along information they’ve received. We could even automate this – the node could just pass the answer from their child up without doing anything if they, in fact, have no knowledge and, presumably, no stake in the outcome:

Here we’ve cleanly passed up Node 8’s confidence to the top node without that pesky trust attenuation problem getting in the way. But we’ve also introduced another obvious problem in that we are simply taking Node 8’s word for it on its 100% confidence level. Clearly we need to reality-check this with a trust factor but we’ve just assigned them all to 1 to avoid attenuation.

We might call this “the biased source problem”. Frequently the people who know anything about an obscure subject are biased because they make their business that subject and have a stake in the outcome. Our best source on Bibi is his golfing buddy at the chamber of commerce. The best source on liver transplants in India is an Indian hepatologist who’d like to do the transplant himself. The results are unrealistically confident answers.

So a variant on this idea is to allow the trust factor of the next-to-last node to stand but ignore the rest by assigning them to 1. This would preserve the trust information of the guy who knows the guy who knows. Here, Node 7’s trust for Node 8 stands (at 70%) but the rest of the nodes are set to 100%:

Another option would be to allow Node 0 to assign a single trust factor to the whole network, perhaps based on how far away the source node (Node 8) is.

In any event, we are short-circuiting our way to the nodes that really matter, the one that knows the guy who knows, and the guy who knows. I think our system should allow this in some form or other. The user would then get an unfiltered opinion on the question at hand.

APPENDIX -- Some math on the asymptote

This is a continuation of the first paragraph of this post. Please read that before trying to understand what's going on here. Also, this is strictly a nerd's eye view of a (very) specific problem. Read it if you're having insomnia.

I don’t have an elegant proof because it’s a crazy amount of algebra, but we can go over some thoughts:

Let’s take a look at the following network:

0 – 1 – 2 – 3

where P=0.6 for all nodes and T=0.7 for all nodes. To roll up the confidence of Node 0 for any given predicate question we can start by computing the confidence of Node 2 after taking into account Node 3. This is just the Bayes eqn. as modified by Sapienza’s trust factor:

P2 = 0.6*(0.5 + (0.6-0.5)T) / (0.6(0.5 + (0.6-0.5)T) + 0.4(0.5+(0.4-0.5)*T)) = 0.6654

We continue by calculating the confidence of Node 1 using the above, just calculated, confidence of Node 2:

P1 = 0.6*(0.5 + (0.6654-0.5)T) / (0.6(0.5 + (0.6654-0.5)T) + 0.4(0.5+(1-0.6654-0.5)*T)) = 0.7062

and so on until we’ve calculated Node 0. If we just substitute T=0.7 into this, we can derive a recurrence relation of the form:

Pnew = (.09 + .42P ) / (.43 + .14P)

That is, the Probability of the next level (new) is a function of the probability of the previous level. The other numbers are just constants associated with the trust (0.7 to keep things simple) and the Pnom (0.5 for a predicate question). P will vary from 0-1, so we can construct a table of Pnew as a function of P:

When T=0.7
P	Pnew
0	0.209302326
0.1	0.297297297
0.2	0.379912664
0.3	0.457627119
0.4	0.530864198
0.5	0.6
0.6	0.66536965
0.7	0.727272727
0.8	0.78597786
0.9	0.841726619
1	0.894736842

We see here that P equal to and below 0.7 results in Pnew > P. Numbers equal to and above 0.8 results in Pnew < P. Therefore, no matter where we start, the recurrence relation will converge somewhere between 0.7-0.8. If we run sapienza_trusttree.py for many nodes (Level = 15) we will obtain P=0.7668. We can also just say Pnew = P in the equation above and solve to get the same result.

When Trust=1, we get the following recurrence relation:

Pnew = 0.6P / (0.2P + 0.4)

Which leads to a table like this:

When T=1
P	Pnew
0	0
0.1	0.142857143
0.2	0.272727273
0.3	0.391304348
0.4	0.5
0.5	0.6
0.6	0.692307692
0.7	0.777777778
0.8	0.857142857
0.9	0.931034483
1	1
1.1	1.064516129
1.2	1.125
1.3	1.181818182

This shows that all values of P above 0 but below 1 increase the resulting Pnew. The asymptote here, of course, is 1 as we already know.

The only difference between these recurrence relations is Trust. Therefore it is trust below 1 which generates a recurrence relation that leads to an asymptote below 1.

Based on this, we can write a general equation as a function of T and P:

Pnew = (0.3 + 0.6T(P-0.5)) / ( (0.3 + 0.6T(P-0.5)) + 0.2 + 0.4*(0.5-P)*T )

If we set Pnew = P, we obtain, after some algebra,

P**2 + P*(2.5/T - 3.5) + (1.5 - 1.5/T) = 0

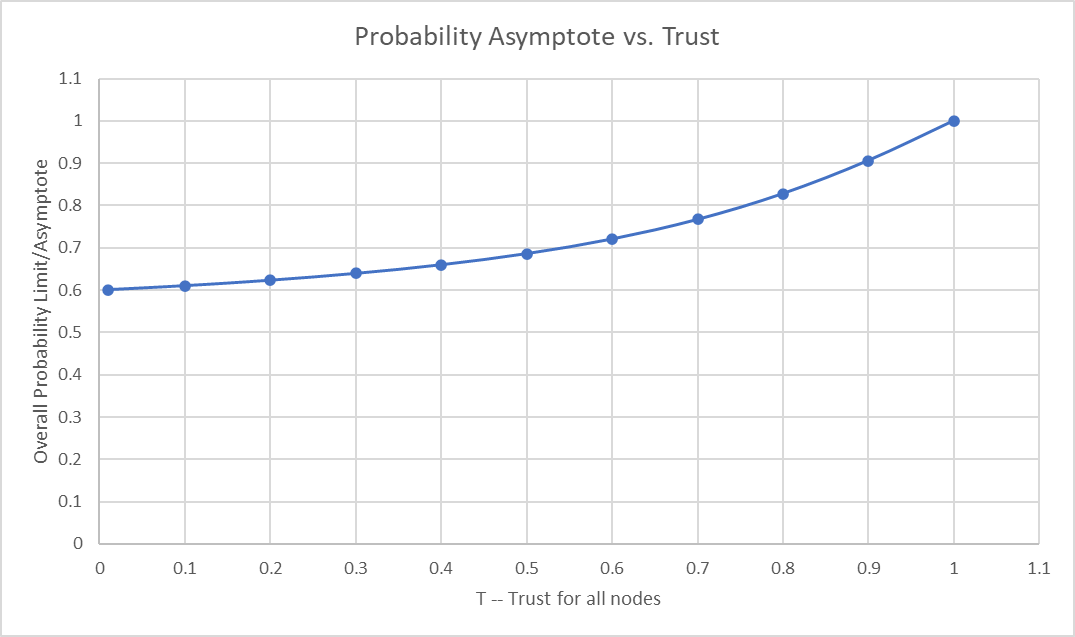
The solution of this equation defines the asymptote (Pasymp), ie the highest probability we can achieve given the trust. It can be solved numerically or using the quadratic formula:

P=( (3.5-2.5/T) +- SQRT((2.5/T - 3.5)*2 - 4(1.5-1.5/T)) ) / 2

T	Pasymp
0.01	0.60096891
0.1	0.610567768
0.2	0.623475383
0.3	0.639520137
0.4	0.659852575
0.5	0.686140662
0.6	0.72075922
0.7	0.766864466
0.8	0.827934423
0.9	0.906150469
1	1

This is not quite a proof but it gives us a more rigorous picture of what’s going on. When trust falls to 0, the confidence of the head node, 0.6, is as good as it gets. If Trust is 1, we will eventually reach P=1 after enough nodes have been factored in. For all T in between, we have a continuously varying degree of P. This makes sense and confirms our initial intuition that a continuous variation in P will result from varying T.